2016安徽高考数学卷,安徽省2016高考数学

1.我是2016届安徽高考的理科生，我的成绩是语文85，数学82，英语103，理综92，高三一年学习没有目标和压力

2.高考数学常用公式及结论

3.2016年高考数学理科全国三卷平均分

4.如何应对2016高考全国卷

118分。《教学考试》是由《教学考试》杂志社于2013年12月出版的图书。截止到2022年10月7日，根据查询历届高考成绩的平均分，2016年高考数学理科全国二卷，是比较简单的，平均分在118分，非常的高，有一半的同学是考的非常好的。

我是2016届安徽高考的理科生，我的成绩是语文85，数学82，英语103，理综92，高三一年学习没有目标和压力

52.39分。根据查询中国教育网显示，2016年高考全国一卷数学总体来说是适中难度，其中题目的提问类型进行创新，据考生透露，其后边的大题文字阅读非常难懂，因次数学平均分只有55.39分。

高考数学常用公式及结论

语文和数学我不知道你们当地的分数能考上二本的分是多少。

反正在我们省内是低的了

理综不用说了。简直低的不像话。

就是多多学习理综的内容吧，。这个网上看什么方法的都是的，都一年过来了。就踏踏实实学什么你心里比谁都清楚。实在不行就问问不好科目的老师。

2016年高考数学理科全国三卷平均分

高中数学公式

抛物线：y = ax *+ bx + c

就是y等于ax 的平方加上 bx再加上 c

a > 0时开口向上

a < 0时开口向下

c = 0时抛物线经过原点

b = 0时抛物线对称轴为y轴

还有顶点式y = a（x+h）* + k

就是y等于a乘以（x+h）的平方+k

-h是顶点坐标的x

k是顶点坐标的y

一般用于求最大值与最小值

抛物线标准方程:y^2=2px

它表示抛物线的焦点在x的正半轴上,焦点坐标为(p/2,0) 准线方程为x=-p/2

由于抛物线的焦点可在任意半轴,故共有标准方程y^2=2px y^2=-2px x^2=2py x^2=-2py

关于圆的公式

体积=4/3(pi）(r^3)

面积=(pi)(r^2)

周长=2(pi)r

圆的标准方程 (x-a)2+(y-b)2=r2 注：（a,b）是圆心坐标

圆的一般方程 x2+y2+Dx+Ey+F=0 注：D2+E2-4F>0

（一）椭圆周长计算公式

椭圆周长公式：L=2πb+4(a-b)

椭圆周长定理：椭圆的周长等于该椭圆短半轴长为半径的圆周长（2πb）加上四倍的该椭圆长半轴长（a）与短半轴长（b）的差。

（二）椭圆面积计算公式

椭圆面积公式： S=πab

椭圆面积定理：椭圆的面积等于圆周率（π）乘该椭圆长半轴长（a）与短半轴长（b）的乘积。

以上椭圆周长、面积公式中虽然没有出现椭圆周率T，但这两个公式都是通过椭圆周率T推导演变而来。常数为体，公式为用。

椭圆形物体 体积计算公式椭圆 的 长半径*短半径*PAI*高

三角函数

两角和公式

sin(A+B)=sinAcosB+cosAsinB sin(A-B)=sinAcosB-sinBcosA

cos(A+B)=cosAcosB-sinAsinB cos(A-B)=cosAcosB+sinAsinB

tan(A+B)=(tanA+tanB)/(1-tanAtanB) tan(A-B)=(tanA-tanB)/(1+tanAtanB)

cot(A+B)=(cotAcotB-1)/(cotB+cotA) cot(A-B)=(cotAcotB+1)/(cotB-cotA)

倍角公式

tan2A=2tanA/(1-tan2A) cot2A=(cot2A-1)/2cota

cos2a=cos2a-sin2a=2cos2a-1=1-2sin2a

sinα+sin(α+2π/n)+sin(α+2π*2/n)+sin(α+2π*3/n)+……+sin[α+2π*(n-1)/n]=0

cosα+cos(α+2π/n)+cos(α+2π*2/n)+cos(α+2π*3/n)+……+cos[α+2π*(n-1)/n]=0 以及

sin^2(α)+sin^2(α-2π/3)+sin^2(α+2π/3)=3/2

tanAtanBtan(A+B)+tanA+tanB-tan(A+B)=0

四倍角公式：

sin4A=-4*(cosA*sinA*(2*sinA^2-1))

cos4A=1+(-8*cosA^2+8*cosA^4)

tan4A=(4*tanA-4*tanA^3)/(1-6*tanA^2+tanA^4)

五倍角公式：

sin5A=16sinA^5-20sinA^3+5sinA

cos5A=16cosA^5-20cosA^3+5cosA

tan5A=tanA*(5-10*tanA^2+tanA^4)/(1-10*tanA^2+5*tanA^4)

六倍角公式：

sin6A=2*(cosA*sinA*(2*sinA+1)*(2*sinA-1)*(-3+4*sinA^2))

cos6A=((-1+2*cosA^2)*(16*cosA^4-16*cosA^2+1))

tan6A=(-6*tanA+20*tanA^3-6*tanA^5)/(-1+15*tanA^2-15*tanA^4+tanA^6)

七倍角公式：

sin7A=-(sinA*(56*sinA^2-112*sinA^4-7+64*sinA^6))

cos7A=(cosA*(56*cosA^2-112*cosA^4+64*cosA^6-7))

tan7A=tanA*(-7+35*tanA^2-21*tanA^4+tanA^6)/(-1+21*tanA^2-35*tanA^4+7*tanA^6)

八倍角公式：

sin8A=-8*(cosA*sinA*(2*sinA^2-1)*(-8*sinA^2+8*sinA^4+1))

cos8A=1+(160*cosA^4-256*cosA^6+128*cosA^8-32*cosA^2)

tan8A=-8*tanA*(-1+7*tanA^2-7*tanA^4+tanA^6)/(1-28*tanA^2+70*tanA^4-28*tanA^6+tanA^8)

九倍角公式：

sin9A=(sinA*(-3+4*sinA^2)*(64*sinA^6-96*sinA^4+36*sinA^2-3))

cos9A=(cosA*(-3+4*cosA^2)*(64*cosA^6-96*cosA^4+36*cosA^2-3))

tan9A=tanA*(9-84*tanA^2+126*tanA^4-36*tanA^6+tanA^8)/(1-36*tanA^2+126*tanA^4-84*tanA^6+9*tanA^8)

十倍角公式：

sin10A=2*(cosA*sinA*(4*sinA^2+2*sinA-1)*(4*sinA^2-2*sinA-1)*(-20*sinA^2+5+16*sinA^4))

cos10A=((-1+2*cosA^2)*(256*cosA^8-512*cosA^6+304*cosA^4-48*cosA^2+1))

tan10A=-2*tanA*(5-60*tanA^2+126*tanA^4-60*tanA^6+5*tanA^8)/(-1+45*tanA^2-210*tanA^4+210*tanA^6-45*tanA^8+tanA^10)

万能公式：

sinα=2tan(α/2)/[1+tan^2(α/2)]

cosα=[1-tan^2(α/2)]/[1+tan^2(α/2)]

tanα=2tan(α/2)/[1-tan^2(α/2)]

半角公式

sin(A/2)=√((1-cosA)/2) sin(A/2)=-√((1-cosA)/2)

cos(A/2)=√((1+cosA)/2) cos(A/2)=-√((1+cosA)/2)

tan(A/2)=√((1-cosA)/((1+cosA)) tan(A/2)=-√((1-cosA)/((1+cosA))

cot(A/2)=√((1+cosA)/((1-cosA)) cot(A/2)=-√((1+cosA)/((1-cosA))

和差化积

2sinAcosB=sin(A+B)+sin(A-B) 2cosAsinB=sin(A+B)-sin(A-B)

2cosAcosB=cos(A+B)-sin(A-B) -2sinAsinB=cos(A+B)-cos(A-B)

sinA+sinB=2sin((A+B)/2)cos((A-B)/2 cosA+cosB=2cos((A+B)/2)sin((A-B)/2)

tanA+tanB=sin(A+B)/cosAcosB tanA-tanB=sin(A-B)/cosAcosB

cotA+cotBsin(A+B)/sinAsinB -cotA+cotBsin(A+B)/sinAsinB

某些数列前n项和

1+2+3+4+5+6+7+8+9+…+n=n(n+1)/2 1+3+5+7+9+11+13+15+…+(2n-1)=n2

2+4+6+8+10+12+14+…+(2n)=n(n+1) 1^2+2^2+3^2+4^2+5^2+6^2+7^2+8^2+…+n^2=n(n+1)(2n+1)/6

1^3+2^3+3^3+4^3+5^3+6^3+…n^3=(n(n+1)/2)^2 1*2+2*3+3*4+4*5+5*6+6*7+…+n(n+1)=n(n+1)(n+2)/3

正弦定理 a/sinA=b/sinB=c/sinC=2R 注： 其中 R 表示三角形的外接圆半径

余弦定理 b2=a2+c2-2accosB 注：角B是边a和边c的夹角

乘法与因式分 a2-b2=(a+b)(a-b) a3+b3=(a+b)(a2-ab+b2) a3-b3=(a-b(a2+ab+b2)

三角不等式 |a+b|≤|a|+|b| |a-b|≤|a|+|b| |a|≤b<=>-b≤a≤b

|a-b|≥|a|-|b| -|a|≤a≤|a|

一元二次方程的解

-b+√(b2-4ac)/2a -b-√(b2-4ac)/2a

根与系数的关系 x1+x2=-b/a x1*x2=c/a 注：韦达定理

判别式 b2-4a=0 注：方程有相等的两实根

b2-4ac>0 注：方程有两个不相等的个实根

b2-4ac<0 注：方程有共轭复数根

立体图形及平面图形的公式

圆的标准方程 (x-a)2+(y-b)2=r2 注：（a,b）是圆心坐标

圆的一般方程 x2+y2+Dx+Ey+F=0 注：D2+E2-4F>0

抛物线标准方程 y2=2px y2=-2px x2=2py x2=-2py

直棱柱侧面积 S=c*h 斜棱柱侧面积 S=c'*h

正棱锥侧面积 S=1/2c*h' 正棱台侧面积 S=1/2(c+c')h'

圆台侧面积 S=1/2(c+c')l=pi(R+r)l 球的表面积 S=4pi*r2

圆柱侧面积 S=c*h=2pi*h 圆锥侧面积 S=1/2*c*l=pi*r*l

弧长公式 l=a*r a是圆心角的弧度数r >0 扇形面积公式 s=1/2*l*r

锥体体积公式 V=1/3*S*H 圆锥体体积公式 V=1/3*pi*r2h

斜棱柱体积 V=S'L 注：其中,S'是直截面面积， L是侧棱长

柱体体积公式 V=s*h 圆柱体 V=pi*r2h

图形周长 面积 体积公式

长方形的周长=（长+宽）×2

正方形的周长=边长×4

长方形的面积=长×宽

正方形的面积=边长×边长

三角形的面积

已知三角形底a，，则S＝ah/2

已知三角形三边a,b,c,半周长p,则S＝ √[p(p - a)(p - b)(p - c)] （海伦公式）（p=(a+b+c)/2）

和：（a+b+c)*(a+b-c)*1/4

已知三角形两边a,b,这两边夹角C，则S＝absinC/2

设三角形三边分别为a、b、c，内切圆半径为r

则三角形面积=(a+b+c)r/2

设三角形三边分别为a、b、c，外接圆半径为r

则三角形面积=abc/4r

已知三角形三边a、b、c,则S＝ √{1/4[c^2a^2-((c^2+a^2-b^2)/2)^2]} (“三斜求积” 南宋秦九韶）

| a b 1 |

S△=1/2 * | c d 1 |

| e f 1 |

| a b 1 |

| c d 1 | 为三阶行列式,此三角形ABC在平面直角坐标系内A(a,b),B(c,d), C(e,f),这里ABC

| e f 1 |

选区取最好按逆时针顺序从右上角开始取，因为这样取得出的结果一般都为正值，如果不按这个规则取，可能会得到负值，但不要紧，只要取绝对值就可以了，不会影响三角形面积的大小！

秦九韶三角形中线面积公式

S=√[(Ma+Mb+Mc)*(Mb+Mc-Ma)*(Mc+Ma-Mb)*(Ma+Mb-Mc)]/3

其中Ma,Mb,Mc为三角形的中线长.

平行四边形的面积=底×高

梯形的面积=（上底+下底）×高÷2

直径=半径×2 半径=直径÷2

圆的周长=圆周率×直径=

圆周率×半径×2

圆的面积=圆周率×半径×半径

长方体的表面积=

（长×宽+长×高＋宽×高）×2

长方体的体积 =长×宽×高

正方体的表面积=棱长×棱长×6

正方体的体积=棱长×棱长×棱长

圆柱的侧面积=底面圆的周长×高

圆柱的表面积=上下底面面积+侧面积

圆柱的体积=底面积×高

圆锥的体积=底面积×高÷3

长方体（正方体、圆柱体）

的体积=底面积×高

平面图形

名称 符号 周长C和面积S

正方形 a—边长 C＝4a

S＝a2

长方形 a和b－边长 C＝2(a+b)

S＝ab

三角形 a,b,c－三边长

h－a边上的高

s－周长的一半

A,B,C－内角

其中s＝(a+b+c)/2 S＝ah/2

＝ab/2?sinC

＝[s(s-a)(s-b)(s-c)]1/2

＝a2sinBsinC/(2sinA)

推论及定理

1 过两点有且只有一条直线

2 两点之间线段最短

3 同角或等角的补角相等

4 同角或等角的余角相等

5 过一点有且只有一条直线和已知直线垂直

6 直线外一点与直线上各点连接的所有线段中，垂线段最短

7 平行公理 经过直线外一点，有且只有一条直线与这条直线平行

8 如果两条直线都和第三条直线平行，这两条直线也互相平行

9 同位角相等，两直线平行

10 内错角相等，两直线平行

11 同旁内角互补，两直线平行

12两直线平行，同位角相等

13 两直线平行，内错角相等

14 两直线平行，同旁内角互补

15 定理 三角形两边的和大于第三边

16 推论 三角形两边的差小于第三边

17 三角形内角和定理 三角形三个内角的和等于180°

18 推论1 直角三角形的两个锐角互余

19 推论2 三角形的一个外角等于和它不相邻的两个内角的和

20 推论3 三角形的一个外角大于任何一个和它不相邻的内角

21 全等三角形的对应边、对应角相等

22边角边公理(sas) 有两边和它们的夹角对应相等的两个三角形全等

23 角边角公理( asa)有两角和它们的夹边对应相等的两个三角形全等

24 推论(aas) 有两角和其中一角的对边对应相等的两个三角形全等

25 边边边公理(sss) 有三边对应相等的两个三角形全等

26 斜边、直角边公理(hl) 有斜边和一条直角边对应相等的两个直角三角形全等

27 定理1 在角的平分线上的点到这个角的两边的距离相等

28 定理2 到一个角的两边的距离相同的点，在这个角的平分线上

29 角的平分线是到角的两边距离相等的所有点的集合

30 等腰三角形的性质定理 等腰三角形的两个底角相等 (即等边对等角）

31 推论1 等腰三角形顶角的平分线平分底边并且垂直于底边

32 等腰三角形的顶角平分线、底边上的中线和底边上的高互相重合

33 推论3 等边三角形的各角都相等，并且每一个角都等于60°

34 等腰三角形的判定定理 如果一个三角形有两个角相等，那么这两个角所对的边也相等（等角对等边）

35 推论1 三个角都相等的三角形是等边三角形

36 推论 2 有一个角等于60°的等腰三角形是等边三角形

37 在直角三角形中，如果一个锐角等于30°那么它所对的直角边等于斜边的一半

38 直角三角形斜边上的中线等于斜边上的一半

39 定理 线段垂直平分线上的点和这条线段两个端点的距离相等

40 逆定理 和一条线段两个端点距离相等的点，在这条线段的垂直平分线上

41 线段的垂直平分线可看作和线段两端点距离相等的所有点的集合

42 定理1 关于某条直线对称的两个图形是全等形

43 定理 2 如果两个图形关于某直线对称，那么对称轴是对应点连线的垂直平分线 44定理3 两个图形关于某直线对称，如果它们的对应线段或延长线相交，那么交点在对称轴上

45逆定理 如果两个图形的对应点连线被同一条直线垂直平分，那么这两个图形关于这条直线对称

46勾股定理 直角三角形两直角边a、b的平方和、等于斜边c的平方，即a^2+b^2=c^2

47勾股定理的逆定理 如果三角形的三边长a、b、c有关系a^2+b^2=c^2 ，那么这个三角形是直角三角形

48定理 四边形的内角和等于360°

49四边形的外角和等于360°

50多边形内角和定理 n边形的内角的和等于（n-2）×180°

51推论 任意多边的外角和等于360°

52平行四边形性质定理1 平行四边形的对角相等

53平行四边形性质定理2 平行四边形的对边相等

54推论 夹在两条平行线间的平行线段相等

55平行四边形性质定理3 平行四边形的对角线互相平分

56平行四边形判定定理1 两组对角分别相等的四边形是平行四边形

57平行四边形判定定理2 两组对边分别相等的四边形是平行四边形

58平行四边形判定定理3 对角线互相平分的四边形是平行四边形

59平行四边形判定定理4 一组对边平行相等的四边形是平行四边形

60矩形性质定理1 矩形的四个角都是直角

61矩形性质定理2 矩形的对角线相等

62矩形判定定理1 有三个角是直角的四边形是矩形

63矩形判定定理2 对角线相等的平行四边形是矩形

64菱形性质定理1 菱形的四条边都相等

65菱形性质定理2 菱形的对角线互相垂直，并且每一条对角线平分一组对角

66菱形面积=对角线乘积的一半，即s=（a×b）÷2

67菱形判定定理1 四边都相等的四边形是菱形

68菱形判定定理2 对角线互相垂直的平行四边形是菱形

69正方形性质定理1 正方形的四个角都是直角，四条边都相等

70正方形性质定理2正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角

71定理1 关于中心对称的两个图形是全等的

72定理2 关于中心对称的两个图形，对称点连线都经过对称中心，并且被对称中心平分

73逆定理 如果两个图形的对应点连线都经过某一点，并且被这一点平分，那么这两个图形关于这一点对称

74等腰梯形性质定理 等腰梯形在同一底上的两个角相等

75等腰梯形的两条对角线相等

76等腰梯形判定定理 在同一底上的两个角相等的梯形是等腰梯形

77对角线相等的梯形是等腰梯形

78平行线等分线段定理 如果一组平行线在一条直线上截得的线段相等，那么在其他直线上截得的线段也相等

79 推论1 经过梯形一腰的中点与底平行的直线，必平分另一腰

80 推论2 经过三角形一边的中点与另一边平行的直线，必平分第三边

81 三角形中位线定理 三角形的中位线平行于第三边，并且等于它的一半

82 梯形中位线定理 梯形的中位线平行于两底，并且等于两底和的一半 l=（a+b）÷2 s=l×h

83 (1)比例的基本性质 如果a:b=c:d,那么ad=bc 如果ad=bc,那么a:b=c:d

84 (2)合比性质 如果a／b=c／d,那么(a±b)／b=(c±d)／d

85 (3)等比性质 如果a／b=c／d=…=m／n(b+d+…+n≠0),那么 (a+c+…+m)／(b+d+…+n)=a／b

86 平行线分线段成比例定理 三条平行线截两条直线，所得的对应线段成比例

87 推论 平行于三角形一边的直线截其他两边（或两边的延长线），所得的对应线段成比例

88 定理 如果一条直线截三角形的两边（或两边的延长线）所得的对应线段成比例，那么这条直线平行于三角形的第三边

89 平行于三角形的一边，并且和其他两边相交的直线，所截得的三角形的三边与原三角形三边对应成比例

90 定理 平行于三角形一边的直线和其他两边（或两边的延长线）相交，所构成的三角形与原三角形相似

91 相似三角形判定定理1 两角对应相等，两三角形相似（asa）

92 直角三角形被斜边上的高分成的两个直角三角形和原三角形相似

93 判定定理2 两边对应成比例且夹角相等，两三角形相似（sas）

94 判定定理3 三边对应成比例，两三角形相似（sss）

95 定理 如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例，那么这两个直角三角形相似

96 性质定理1 相似三角形对应高的比，对应中线的比与对应角平分线的比都等于相似比

性质定理2 相似三角形周长的比等于相似比

98 性质定理3 相似三角形面积的比等于相似比的平方

99 任意锐角的正弦值等于它的余角的余弦值，任意锐角的余弦值等

于它的余角的正弦值

100任意锐角的正切值等于它的余角的余切值，任意锐角的余切值等于它的余角的正切值

101圆是定点的距离等于定长的点的集合

102圆的内部可以看作是圆心的距离小于半径的点的集合

103圆的外部可以看作是圆心的距离大于半径的点的集合

104同圆或等圆的半径相等

105到定点的距离等于定长的点的轨迹，是以定点为圆心，定长为半径的圆

106和已知线段两个端点的距离相等的点的轨迹，是着条线段的垂直平分线

107到已知角的两边距离相等的点的轨迹，是这个角的平分线

108到两条平行线距离相等的点的轨迹，是和这两条平行线平行且距离相等的一条直线

109定理 不在同一直线上的三点确定一个圆。

110垂径定理 垂直于弦的直径平分这条弦并且平分弦所对的两条弧

111推论1 ①平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧

②弦的垂直平分线经过圆心，并且平分弦所对的两条弧

③平分弦所对的一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧

112推论2 圆的两条平行弦所夹的弧相等

113圆是以圆心为对称中心的中心对称图形

114定理 在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等，所对的弦的弦心距相等

115推论 在同圆或等圆中，如果两个圆心角、两条弧、两条弦或两弦的弦心距中有一组量相等那么它们所对应的其余各组量都相等

116定理 一条弧所对的圆周角等于它所对的圆心角的一半

117推论1 同弧或等弧所对的圆周角相等；同圆或等圆中，相等的圆周角所对的弧也相等

118推论2 半圆（或直径）所对的圆周角是直角；90°的圆周角所 对的弦是直径

119推论3 如果三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形

120定理 圆的内接四边形的对角互补，并且任何一个外角都等于它的内对角

121①直线l和⊙o相交 d＜r

②直线l和⊙o相切 d=r

③直线l和⊙o相离 d＞r

122切线的判定定理 经过半径的外端并且垂直于这条半径的直线是圆的切线

123切线的性质定理 圆的切线垂直于经过切点的半径

124推论1 经过圆心且垂直于切线的直线必经过切点

125推论2 经过切点且垂直于切线的直线必经过圆心

126切线长定理 从圆外一点引圆的两条切线，它们的切线长相等，圆心和这一点的连线平分两条切线的夹角

127圆的外切四边形的两组对边的和相等

128弦切角定理 弦切角等于它所夹的弧对的圆周角

129推论 如果两个弦切角所夹的弧相等，那么这两个弦切角也相等

130相交弦定理 圆内的两条相交弦，被交点分成的两条线段长的积相等

131推论 如果弦与直径垂直相交，那么弦的一半是它分直径所成的

两条线段的比例中项

132切割线定理 从圆外一点引圆的切线和割线，切线长是这点到割

线与圆交点的两条线段长的比例中项

133推论 从圆外一点引圆的两条割线，这一点到每条割线与圆的交点的两条线段长的积相等

134如果两个圆相切，那么切点一定在连心线上

135①两圆外离 d＞r+r ②两圆外切 d=r+r

③两圆相交 r-r＜d＜r+r(r＞r)

④两圆内切 d=r-r(r＞r) ⑤两圆内含d＜r-r(r＞r)

136定理 相交两圆的连心线垂直平分两圆的公共弦

137定理 把圆分成n(n≥3):

⑴依次连结各分点所得的多边形是这个圆的内接正n边形

⑵经过各分点作圆的切线，以相邻切线的交点为顶点的多边形是这个圆的外切正n边形

138定理 任何正多边形都有一个外接圆和一个内切圆，这两个圆是同心圆

139正n边形的每个内角都等于（n-2）×180°／n

140定理 正n边形的半径和边心距把正n边形分成2n个全等的直角三角形

141正n边形的面积sn=pnrn／2 p表示正n边形的周长

142正三角形面积√3a／4 a表示边长

143如果在一个顶点周围有k个正n边形的角，由于这些角的和应为

360°，因此k×(n-2)180°／n=360°化为（n-2）(k-2)=4

144弧长计算公式：l=nπr／180

145扇形面积公式：s扇形=nπr2／360=lr／2

146内公切线长= d-(r-r) 外公切线长= d-(r+r)

147等腰三角形的两个底脚相等

148等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合

149如果一个三角形的两个角相等，那么这两个角所对的边也相等

150三条边都相等的三角形叫做等边三角形

如何应对2016高考全国卷

118分。普通高等学校招生全国统一考试 (全国卷 Ⅲ)·理科数学 总分数 170分，2016年高考数学理科全国三卷平均分是118分，理科学科主要有：数学、物理学、化学、生物学、地理学、计算机软件应用、技术与设计实践等。

随 着一系列高考新政的出台，年复一年的全国高考正在发生引人注目的变化。2014年《院关于深化考试招生制度改革的实施意见》公布后，恢复“全国一张 卷”成为改革大趋势。2015年，使用全国统一命题试卷的省份增至18个(新增江西、辽宁、山东3省)，2016年将有26个省份(新增福建省、广东省、 四川省、陕西省、安徽省、湖南省、湖北省、重庆市)使用统一命题试卷。全国统一命题试卷相对于这些自主命题省份的试卷到底有何变化呢？这些省份的考生应该 怎样备考2016年高考呢？下面高考君就为你举例解析。

如何应对2016高考全国卷？

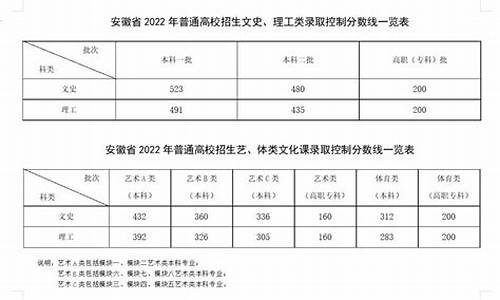
安徽：政治学科更注重探究性试题

2016 年起，安徽高考文综考试将统一使用全国新课标卷(以下简称全国卷)，这意味着自2009年以来的安徽文综自主命题正式落下帷幕。全国卷共有Ⅰ卷与Ⅱ卷两套 试题，到目前为止，安徽省高考使用其中哪一套教育部还没有最终定调。但从安徽省属于华东地区，基础教育相对发达的现实来看，使用Ⅰ卷的概率更大。

与 安徽卷相比，全国卷政治学科试题有浓郁的开放性、探究性和思辨性，如2013年全国Ⅰ卷第39题(1)问“你是赞成还是反对《现代汉语词典》收录西文字母 词？请用《文化生活》的有关知识阐明理由。”这一“两难性”试题(借鉴了辩论赛的合理要素，创设两难情境，让学生在两种对立的观点中做出选择并说明理由) 的命制。又如，2014年全国Ⅰ卷第39题(3)问“结合材料，就教育创新拟定两条公益广告词，要求主题鲜明、朗朗上口，每条限15个字以内。”再 如，2015年全国Ⅰ卷第39题(3)问“在城镇化快速发展的今天，请就如何记住乡愁提出两条建议。”

这体现了全国卷注重考查知识在现实中的具体运用，注重考查考生论证和探究问题的能力，注重考查考生在分析、解决问题中所能展现的创新意识、科学精神和发散思维，真正体现新课程所倡导的开放、自主、探究的理念，答案的不固定性和不唯一性极大地释放了学生的思维张力和韧性。

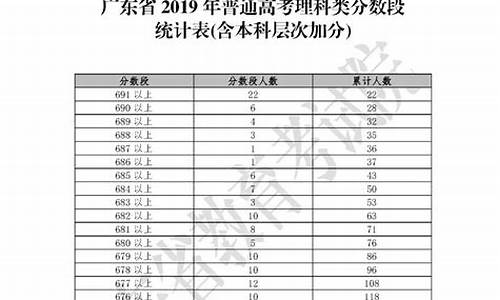
广东：分值题型有变，难度有所增加

2014 年广东语文高考大纲与2015年全国新课标大纲的《考试说明》要求基本一致，两者不同点主要体现在试卷结构、具体题型分值分布上，部分题型也有变化。广东 省某重点中学的肖老师认为，从2014年、2015年新课标卷《考试说明》题型示例的不同点，可以给广东2016年备考带来启示。

在 理科数学上，广东卷和新课标虽然考点接近，但是考点所放的位置不同，导致了对知识点的能力要求产生了变化。例如广东卷中一直屹立不倒的简答题“三角函 数”，在新课标中“降级”为小题，但题量增加至3道，因此，更要求学生掌握三角当中的一些原理问题。而数列题放在了简答题中的第一道，立体几何的要求也有 所提升。数学一直是文科生的“痛”，广东高考改革以后，对文科生利好的消息是数学小题的分值增加了，由原来的“10选择4填空”总分值70分，增加为 “12选择4填空”总分值80分。对于一些平时做题细心，重视基础的学生是利好。

四川：或用中等难度卷

全国卷咋命题？根据难度命两套题，四川或用中等难度的全国2卷

三主科怎么变？

语文卷：难度加大、题型有变化。

语 文全国卷中，大阅读题分为必考和选考，有实用性文本和文学类文本供学生选择，四川卷近年来均为文学类文本，考生的复习也都倾向于这方面。“高三的时候，考 生不能把全部时间用来刷题提升考试技巧，应该空出一部分时间提升阅读能力和语文素养。同时还要注意文言文和诗歌内容的复习。”有老师表示，总体来说，全国 卷要比四川卷难一些。

数学卷：多一道题和选修内容。针对这一变化，即将步入高三的学生们，一方面要把基础打扎实，把全国卷要考的选修的内容也学习一下，另一方面，可以多练习一些沿海的新题型，比如数学在实际生活中的应用等。

英语卷：听力30分作文变25分。

针 对这一变化，成都某中学英语老师建议考生，在平时的学习与备考中，熟悉重音、语调等相关语音知识，加强辨音能力；重点对归纳信息、推断说话者意图、观点和 态度的试题进行练习；广泛接触各种日常话题和各方面的题材，可以尝试多接触VOA、BBC、CNN等新闻听力，精听与泛听双管齐下，提升在听的过程中记关 键词的能力，也可以尝试通过练习听写文章的方式不断提升听力水平。

重庆：语数外有较大变化

数学：客观题增加总题目数增加1道

目前，重庆卷数学学科题型理科是10道单选题、5道填空题(6选5)、6道解答题；文科题型为10道单选题、5道填空题和6道解答题，文理科总题目数均为21道。但在用全国卷后，会增加为22道。

“单选题增加为12道，填空题减少为4道且没有选做题；但文理科解答题均有5道必做题和一道‘3选1’的题目。”某位老师介绍，使用全国卷后，尽管增加了解答题的选做题，但同时客观题的数量也有所增加，因此，难度其实是持平的。

建议：考生在应考过程中，还是应该以基础题为核心，同时注意留心解题过程中的方法和关系，做到活学活用。

语文：古诗词、文言文要求提高

重庆育才中学高一年级语文备课组组长刘老师认为，这次的高考改革其实是在意料之中，考生和家长在心态上不必恐慌。

“全 国卷一开始就是社科文阅读，而重庆自主命题的语文试卷则将字音字形题放在开篇，相对来说要平稳一些。”刘老师说，与重庆卷相比，全国卷为理解性默写，要求 学生必背的古诗文增加；重庆卷阅读全是文学类主观题型，而全国卷则为文学文本阅读或者实用文本阅读，分为主观和客观两种题型。

建议：考生可以加强古诗词、文言文的阅读和理解，提高阅读能力。

福建：考查重点或有不同

2016 年福建省高考所有科目将统一使用全国卷，阅卷和录取依然由福建省组织开展。至于到底是使用全国Ⅰ卷还是Ⅱ卷，还要等教育部门的最后配套文件。卸掉高考命题 重担后，福建省教育招生考试部门的精力将会更多集中在高中学业水平测试上，为几年后的福建省“新高考”(考试招生制度改革)做准备。

“全国卷”和“福建卷”到底有何不同？就语文学科来说，福建自主命题有本省特色，重视文化经典和文学名著，淡化语基；而全国卷，特别是全国Ⅰ卷的语文，有单独的语基题，且阅读也相对较难。

今年5月底，在有关单位举行的研讨会上，多名专家指出，“全国卷”不能简单地用“容易”或“难”来做出判断，高考要考查的知识不会因为出题方的变化而有大的变动，考生只要按照认真复习备考即可。

陕西：听力计入成绩总分

从 2016年起，陕西省高考将全部使用全国卷，且英语考试中的听力考试成绩也将计入外语科总分之中。日前，陕西省招办新闻发言人张军利对媒体介绍，从 2016年起，陕西省普通高校招生统考将全部使用教育部统一命制的试题，也就是通常所说的“全国卷”。“‘全国卷’带来的最大变化就是外语科目含有听力部 分，而且听力成绩要计入高考外语科总分。”张军利说。据了解，高考英语听力考试恢复后，将取国家教育考试标准化考点语音广播系统统一播放考试内容的方式 进行。

鉴 于陕西省高考外语听力考试已经停考多年，为确保恢复听力考试平稳顺利进行，陕西省教育厅近日下发通知，要求各市、县(区)要切实加强对辖区内普通高中的外 语教学管理，尽快部署普通高中学校严格按照教学大纲要求，组织好外语教学活动，培养和提高高中学生外语听说读写能力。平时以及学期、学年的外语科目考试 中，都应有听力测试内容。

这也启示陕西省的考生平时要加强听力训练。

湖南：注意全国卷的开放性的题目

全国卷的热点与湖南卷有所不同，从全国卷命题趋势来看，未来可能会用一些开放性的题目，更有利于推动素质教育发展，也有利于考查学生的综合素质。全国卷的命题水平也远高于以前，对于考生来说，这样的命题方式更加公平。

现在高一和高二的学生要“何去何从”？跟着老师的节奏走就好。高考不管怎么改，考试的内容都是万变不离其宗，只要按照新课标的要求掌握知识，不管怎么考，都没多大区别。

湖北：语文试题结构变化大

2016 年高考所有科目都使用全国卷后，考试内容、题型将会有变化呢。据业内人士分析：首先是语文考试试题结构将发生较大变化。目前高中阶段学生所使用的是新课标 教材。全国高考语文试卷分为两大类为新课标卷和全国大纲卷，从2004年开始到2014年，湖北省高考语文所使用的试卷与全国大纲卷试题结构相似。但是 用新课标试卷后，试题结构将完全改变。

荆 州中学高一语文备课组组长周贤介绍，新课标卷分第一卷和第二卷，第一卷分值在70分，直接取名为阅读部分，第二卷叫做表达部分。卷一分必做题和选做题，必 做题里面分为现代文阅读和古诗文阅读，选做部分又分两大类，一个是文学类作品，一个是实用类作品，只需要选做一道题目。

周老师表示，与之前的语文试卷相比较，新课标试卷更注重学生课外阅读能力和阅读数量，学生不能只局限于课堂上对基础知识的死记硬背。

和语文不一样，数学试卷方面题型基本不变，仍然是考选择、填空和解答三类题型，但是在题目数量上略微有所调整。另外，无论是全国卷还是湖北省考卷，在数学知识考察上，还是以基础知识为主，全国卷则更加注重考生对数学知识的应用。

荆州中学数学备课组组长马玮表示，题型的难易程度，不太好预估，但是从多年来看，总体来讲湖北卷子和全国相比的话，全国卷子相对平和一些，可能会打破考生多年来对数学考试的恐惧和无奈。

外语方面，在题型上没有了多项选择题和完成句子等题型，但是增加了阅读理解7选5 、词汇语法填空和短文改错等题型。题型的变化，更加要求学生英语应用综合能力的提高。