高考几何大题及答案_高考解析几何大题45道及答案

1.2011辽宁高考数学 理科 立体几何题 用几何法做（答案给的是向量法) 题目见问题补充

2.高中数学求2010课标全国卷高考立体几何题 求几何解法，不要向量解法

3.2011安徽高考理数空间几何那大题怎么证明BCEF四点共面？！！

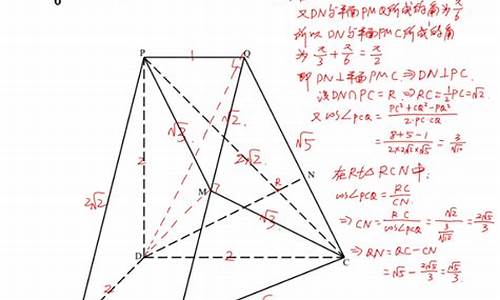
解析几何一般考察：

直线的斜率问题，其中包括直线垂直，直线平行！使用解析几何的公式！

直线与圆的位置关系，转化成求德尔塔的值。

直线与双曲线，椭圆，抛物线的位置关系。

直线关于直线对称。

点关于直线对称。

圆关于直线对称，

还要了解所有数学表达式的几何意义。

重要的是理解数学的转化思想

2011辽宁高考数学 理科 立体几何题 用几何法做（答案给的是向量法) 题目见问题补充

1：过M作AB的垂线MD，并连接CD、SD。则有MD//=1/2AP。=》MD垂直于面ABC，=》MD的垂直于SN。而AC=1/2AB=》 AD=AB 。所以<ADB=45。又有SD=1/2AB、ND=NA=1/2AB。所以<DNS=45。（能推出NS的长度为二分之根号二，第二问用到。）所以就有CD垂直于NS。所以NS垂直于面CDM，所以CM垂直于SN。

2：根据：V(M-CNS)=V(S-CMN)可以求求得点S到平面CMN的距离，而由第一问中得出的NS的长度。即可用三角函数把角表示出来。

高中数学求2010课标全国卷高考立体几何题 求几何解法，不要向量解法

(1)证明：∵四边形ABCD为正方形，PD⊥平面ABCD，PD∥QA，QA=AB=PD．

∴AD=AQ，∠QAD=90°

过Q作QE⊥PD交PD于E

平面PQC⊥平面DCQ；

∴E为PD中点==>QD=QP，QD⊥QP

易知CD⊥面AQPD==>CD⊥PQ

∴PQ⊥面CDQ

∴面PQC⊥面CDQ

(2)解析：设ABCD边长为1

易知BC⊥面PCD==>BC⊥PC

∴BC=CD=1，PD=2==>PC=√5==>PB=√6

过C作CF⊥PB交PB于F，过Q作QG⊥PB交PB于G，过F作HF//QG交QB于H,连接HC

∴∠CFH为二面角Q-BP-C的平面角

BC^2=BF*BP==>1=BF*√6==>BF=√6/6==>CF=√(BC^2-BF^2)=√30/6

易知BQ=DQ=PQ=√2

∴G为PB中点

QG=√(BQ^2-BG^2)=√2/2

⊿BFH∽⊿BGQ==>BF/BG=FH/QG=BH/BQ

∴HF=√2/6，BH=√2/3

∵BC⊥BQ

∴CH=√(BC^2+BH^2)=√11/3

由余弦定理HC^2=FC^2+FH^2-2*FC*HF*cos∠CFH

11/9=5/6+1/18-2*√30/6*√2/6*cos∠CFH

cos∠CFH=-√15/5

∴二面角Q—BP—C的余弦值为-√15/5．

2011安徽高考理数空间几何那大题怎么证明BCEF四点共面？！！

我来帮你解，

做辅助线：延长EH交BC与点F。

∵EH是直角△EAD中线，

∴DE=EA=EH，

∴∠EDH=∠DHE，∵∠EHD=∠BHF，∴∠ADH=∠BHF

又∵四边形是等腰梯形，∴∠DAC=∠DBC

∴△DAH≌△BHF，

∴EF⊥BC

又∵PH⊥面ABCD，∴PH⊥BC，

∴面PEF⊥BC，

∴PE⊥BC.

设AB=x，过A点做BC的平行线延长EF交于点H。

∵面PEF⊥BC，∴AG⊥面PEF，

∴即求角APG的正弦

由题意得AG=√2x/4，AH=√2x/2，PA=x，PH=√2x/2，GH=√6x/4,PG=√PH^2+GH^2=√14x/4,

sin∠APG=√7/7.

设 G 是线段 DA 与线段 EB 延长线的交点，由于△OAB 与△ODE 都是正三角形，所以 OB ∥ ,OB= ,OG=OD=2 同理，设 G′是线段 DA 与线段 FC 延长线的交点，有 OG′=OD=2，又由于 G 和 G′都在线段 DA 的延长线上，所以 G 与 G′重合。 在△GED 和△GFD 中，由 OB∥ ,OB= 和 OC∥ , OC= ,可知 B,C 分别是 GE 和 GF 的中点，所以 BC 是△GEF 的中位线，故 BC∥EF. （向量法） 过点 F 作 FQ⊥AD,交 AD 于点 Q，连 QE，由平面 ABED⊥平面 ADFC，知 FQ⊥平面 ABED,以 Q 为 坐标原点， 标系。 为 x 轴正向， 为 y 轴正向， 为 z 轴正向，建立如图所示空间直角坐 由条件知 E( ，0,0)，F（0,0， ），B（ ，- ，0），C（0，- ， ）。 则有， ， 。 所以 ，即得 BC∥EF. 所以bcef共面