2017年高考数学3_2017年高考数学二卷

1.2017高考总分多少

2.2017年数学高考考纲和16年的区别

3.2017年数学高考卷子的六道大题

4.2017年各省高考总分分别是多少

5.2017年高考数学平面向量必考知识点

6.2017年高考理科数学22题。 第二问最后一步怎么求的a的值？其余步骤我都

7.2017年全国一卷数学高考题，如图，答案最后为什么写m＞负一？

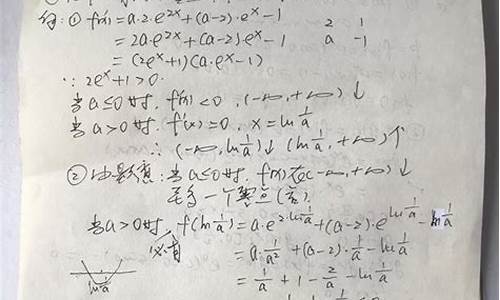
不大。根据查询贵州教育局官网得知，2017年贵州省普通高考数学题难度不大，没有偏难怪题，区分度较好，试卷所考查的知识和能力符合考试大纲的内容和要求。普通高等学校招生全国统一考试简称高考，是中华人民共和国合格的高中毕业生或具有同等学力的考生参加的选拔性考试。

2017高考总分多少

2017年各省份试卷使用情况

　全国Ⅰ卷地区：

福建、河南、河北、山西、江西、湖北、湖南、广东、安徽

　全国Ⅱ卷地区：

甘肃、青海、内蒙古、黑龙江、吉林、辽宁、宁夏、新疆、 *** 、陕西、重庆

　全国Ⅲ卷地区：

云南、广西、贵州、四川

　自主命题省份

自主命题：江苏、北京、天津、上海

　部分使用全国卷省份

海南省：全国Ⅱ卷(语、数、英)单独命题(政、史、地、物、化、生)

山东卷：全国Ⅰ卷(外语、文综、理综)自主命题(语文、文数、理数)

　2017年高考改革地区：浙江、上海

1.考试模式：3+3，不分文理科

2.必考科目：语文、数学、外语，每科150分

3.外语考试：

浙江每年2次，6月和10月;上海每年2次，1月和6月。

4.选考科目：

浙江实行7选3，每科满分100分：思想政治、历史、地理、物理、化学、生物、信息技术(特别说明：浙江省的选考科目考试次数为2次，分别在4月和10月，外语和选考成绩2年有效。

)

上海实行6选3，每科满分70分，思想政治、历史、地理、物理、化学、生命科学。

2017年数学高考考纲和16年的区别

国内不同省份的具体高考政策有所不同，就大部分使用全国卷的省份而言，高考的总分是750分，因此，2017年高考的总分也是750分。

高考总分为750分的大部分省份，其分数构成为：

语文150分，数学150分，外语150分，综合300分。

全国卷：

是教育部考试中心组织命制的适用于全国大部分省区的高考试卷，目的在于保证人才选拔的公正性。从2016年开始，全国Ⅰ、Ⅱ、Ⅲ卷分别改称为全国乙、甲、丙卷。

小语种（日语/俄语/法语/德语/西班牙语）高考统一使用全国卷，各省均无自主命题权，且不分甲乙丙卷。

参考资料：

百度百科-全国卷

2017年数学高考卷子的六道大题

1、增加了数学文化的要求。

2、在能力要求内涵方面，增加了基础性、综合性、应用性、创新性的要求，同时对能力要求进行了加细说明，使能力要求更加明确具体。

3、在现行考试大纲三个选考模块中删去《几何证明选讲》，其余2个选考模块的内容和范围都不变，考生从《坐标系与参数方程》、《不等式选讲》2个模块中任选1个作答。

总体上，这些变化对2017年高考数学考试影响不大。基于两个原因：

一是在这次高考考纲修订基本原则 “坚持整体稳定，推进改革创新；优化考试内容，着力提高质量；提前谋篇布局，体现素养导向”中，将“整体稳定”放在了首位。2015年、2016年全国数学2卷就突出了稳中求变，约有80%的试题是稳定的，只有约20%的试题是创新的，2017年高考仍然还会沿用这种思路命制试卷。

二是近两年高考试卷已先于2017年高考考纲在命题中渗透了一些变化与创新，全国数学2卷最大的变化点是，突出了社会主义核心价值观，强调了中国传统数学文化精髓。在数学文化方面，2016年高考全国2卷理科数学第8题、文科数学第9题涉及到了我国南宋著名数学家秦九韶提出的多项式求值的算法，2015年高考全国2卷文、理科数学的第8题涉及到了我国古代数学名著《九章算术》中的“更相减损术”。

这就是说，今年考纲中所提到的新要求、新变化，在两年前的高考中就已经有所体现了，所以2017年高考对我们而言变化不会很大。而第三项变化是选考题由“三选一”变为“二选一”，这将减轻学生的课业负担。

2017年各省高考总分分别是多少

17.（12分）

△ABC的内角A，B，C的对边分别为a，b，c，已知△ABC的面积为

（1）求sinBsinC;

（2）若6cosBcosC=1,a=3,求△ABC的周长

18.（12分）

如图，在四棱锥P-ABCD中，AB//CD，且

(1)证明：平面PAB⊥平面PAD；

(2)若PA=PD=AB=DC,,求二面角A-PB-C的余弦值.

19．（12分）

为了监控某种零件的一条生产线的生产过程，检验员每天从该生产线上随机抽取16个零件，并测量其尺寸（单位：cm）．根据长期生产经验，可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布N(μ,σ?)．

（1）假设生产状态正常，记X表示一天内抽取的16个零件中其尺寸在(μ–3σ,μ+3σ)之外的零件数，求P(X≥1)及X的数学期望；学科&网

（2）一天内抽检零件中，如果出现了尺寸在(μ–3σ,μ+3σ)之外的零件，就认为这条生产线在这一天的生产过程可能出现了异常情况，需对当天的生产过程进行检查．

（ⅰ）试说明上述监控生产过程方法的合理性；

（ⅱ）下面是检验员在一天内抽取的16个零件的尺寸：

9.95

10.12

9.96

9.96

10.01

9.92

9.98

10.04

10.26

9.91

10.13

10.02

9.22

10.04

10.05

9.95

经计算得，，其中xi为抽取的第i个零件的尺寸，i=1,2,…,16．

用样本平均数作为μ的估计值，用样本标准差s作为σ的估计值，利用估计值判断是否需对当天的生产过程进行检查？剔除之外的数据，用剩下的数据估计μ和σ（精确到0.01）．

附：若随机变量Z服从正态分布N(μ,σ2)，则P(μ–3σ<Z<μ+3σ)=0.997?4，0.997?416≈0.959?2，．

20.（12分）

已知椭圆C：x?/a?+y?/b?=1（a>b>0），四点P1（1,1），P2（0,1），P3（–1，√3/2），P4（1，√3/2）中恰有三点在椭圆C上.

（1）求C的方程；

（2）设直线l不经过P2点且与C相交于A，B两点.若直线P2A与直线P2B的斜率的和为–1，证明：l过定点.

21.（12分）

已知函数=ae?^x+（a﹣2）e^x﹣x.

（1）?讨论的单调性；

（2）?若有两个零点，求a的取值范围.

（二）选考题：共10分。

请考生在第22、23题中任选一题作答，如果多做，则按所做的第一题计分。

22．[选修4-4，坐标系与参数方程]（10分）

在直角坐标系xOy中，曲线C的参数方程为（θ为参数），直线l的参数方程为.

（1）若a=-1，求C与l的交点坐标；

（2）若C上的点到l的距离的最大值为，求a.

23.[选修4—5：不等式选讲]（10分）

已知函数f（x）=–x?+ax+4，g(x)=│x+1│+│x–1│.

（1）当a=1时，求不等式f（x）≥g（x）的解集；

（2）若不等式f（x）≥g（x）的解集包含[–1，1]，求a的取值范围.

2017年高考数学平面向量必考知识点

　2017年高考已经结束了，那么2017年高考总分多少分?各科的总分都是多少?下面是我整理的2017年各省高考总分，希望能给大家带来帮助!

　 2017年各省高考总分

　就全国的形式来讲，大部分地区的总分值还是一样的，如：安徽、北京、福建、甘肃、广东、广西、贵州、河北、河南、黑龙江、湖北、湖南、吉林、江西、辽宁、内蒙、宁夏、青海、山东、山西、陕西、四川、天津、西藏、新疆、云南、重庆等27个省市还是750分满分。各科的分值详情如下：语文150分，数学150分，英语150分，文综/理综300分。

　个别改革地区的分值详情需要大家做详细的了解，比如江苏、上海、浙江和海南这4个地区：

　浙江地区的高考总分：

　上海和浙江地区2017年采用的是3+3考试模式，即3门必考科目(语文、数学、英语)+选考科目，我们先来看浙江地区的总分：

　其中语文、数学和外语三科满分各为150分，其中英语笔试满分120分，英语听力考试满分30分;综合(文/理)满分300分;自选模块满分60分;技术满分100分，由通用技术和信息技术两科目成绩按各占50%的比例合成。

　需要特别提醒大家的是浙江的总分根据大家的选择而有所差异，即考生文化成绩总分按报考(含兼报)的不同考试类别分别合成。文理科一类为“3+综合+自选模块”的总分，满分为810分;二类为“3+综合”的总分，满分为750分;三类为“3+技术”的总分，满分为550分。

　上海地区的高考总分：

　2017年上海高考成绩满分660分，各科的分值详情是这样的哦：语文、数学(文/理)、外语满分均为150分，政治、历史、地理、物理、化学、生物任选3门：每门70分。

　 江苏地区的高考总分：　　

　江苏同样采用的是必考+选考模式，其中统考科目为语文、数学、外语三门，各科分值设定为：语文160分，数学160分，外语120分，共440分。语文、数学分别另设附加题40分，总分480分。

　选测科目各科满分为120分，按考生成绩分布分为A+、A、B+、B、C、D六个等级。

　 海南地区的高考总分：

　2017年海南的总分以900分的满分当之无愧的位据全国首位，语文、数学(文)、数学(理)、英语等科目的满分值均为150分，其中，英语科分听力和笔试两部分，笔试部分满分值为120分，听力部分满分值为30分，听力成绩计入英语科总分。政治、历史、地理、物理、化学、生物等科目的满分值均为100分，

2017年高考理科数学22题。 第二问最后一步怎么求的a的值？其余步骤我都

　平面向量是在二维平面内既有方向又有大小的量，物理学中也称作矢量，与之相对的是只有大小、没有方向的数量。以下是我为您整理的关于2017年高考数学平面向量必考知识点的相关资料，希望对您有所帮助。

　高考数学必考知识点平面向量概念：

　(1)向量：既有大小又有方向的量。向量不能比较大小，但向量的模可以比较大小。

　(2)零向量：长度为0的向量，记为0，其方向是任意的，0与任意向量平行。

　(3)单位向量：模为1个单位长度的向量

　(4)平行向量：方向相同或相反的非零向量

　(5)相等向量：长度相等且方向相同的向量

　高考数学必考知识点平面向量数量积解析

　1、平面向量数量积：已知两个非零向量a、b，那么|a||b|cos?(?是a与b的夹角)叫做a与b的数量积或内积，记作a?b。零向量与任意向量的数量积为0。数量积a?b的几何意义是：a的长度|a|与b在a的方向上的投影|b|cos?的乘积。

　两个向量的数量积等于它们对应坐标的乘积的和。即：若a=(x1,y1),b=(x2,y2)，则a?b=x1?x2+y1?y2

　2、平面向量数量积具有以下性质：

　1、a?a=|a|2?0

　2、a?b=b?a

　3、k(a?b)=(ka)b=a(kb)

　4、a?(b+c)=a?b+a?c

　5、a?b=0<=>a?b

　6、a=kb<=>a//b

　7、e1?e2=|e1||e2|cos?

　高考数学必考知识点平面向量加法解析

　已知向量AB、BC，再作向量AC，则向量AC叫做AB、BC的和，记作AB+BC，即有：AB+BC=AC。

　注：向量的加法满足所有的加法运算定律，如：交换律、结合律。

　高考数学必考知识点平面向量减法解析

　1、AB-AC=CB，这种计算法则叫做向量减法的三角形法则，简记为：共起点、指被减。

　-(-a)=a;a+(-a)=(-a)+a=0;a-b=a+(-b)。

　平面向量公式汇总

　1、定比分点

　定比分点公式(向量P1P=?向量PP2)

　设P1、P2是直线上的两点，P是l上不同于P1、P2的任意一点。则存在一个实数 ?，使 向量P1P=?向量PP2，?叫做点P分有向线段P1P2所成的比。

　若P1(x1,y1)，P2(x2,y2)，P(x,y)，则有

　OP=(OP1+?OP2)(1+?);(定比分点向量公式)

　x=(x1+?x2)/(1+?),

　y=(y1+?y2)/(1+?)。(定比分点坐标公式)

　我们把上面的式子叫做有向线段P1P2的定比分点公式

　2、三点共线定理

　若OC=?OA +?OB ,且?+?=1 ,则A、B、C三点共线

　三角形重心判断式

　在△ABC中，若GA +GB +GC=O,则G为△ABC的重心

　[编辑本段]向量共线的重要条件

　若b?0，则a//b的重要条件是存在唯一实数?，使a=?b。

　a//b的重要条件是 xy'-x'y=0。

　零向量0平行于任何向量。

　[编辑本段]向量垂直的充要条件

　a?b的充要条件是 a?b=0。

　a?b的充要条件是 xx'+yy'=0。

　零向量0垂直于任何向量.

　设a=(x，y)，b=(x'，y')。

　3、向量的加法

　向量的加法满足平行四边形法则和三角形法则。

　AB+BC=AC。

　a+b=(x+x'，y+y')。

　a+0=0+a=a。

　向量加法的运算律：

　交换律：a+b=b+a;

　结合律：(a+b)+c=a+(b+c)。

　4、向量的减法

　如果a、b是互为相反的向量，那么a=-b，b=-a，a+b=0. 0的反向量为0

　AB-AC=CB. 即?共同起点，指向被减?

　a=(x,y) b=(x',y') 则 a-b=(x-x',y-y').

　5、数乘向量

　实数?和向量a的乘积是一个向量，记作?a，且∣?a∣=∣?∣?∣a∣。

　当?>0时，?a与a同方向;

　当?<0时，?a与a反方向;

　当?=0时，?a=0，方向任意。

　当a=0时，对于任意实数?，都有?a=0。

　注：按定义知，如果?a=0，那么?=0或a=0。

　实数?叫做向量a的系数，乘数向量?a的几何意义就是将表示向量a的有向线段伸长或压缩。

　当∣?∣>1时，表示向量a的有向线段在原方向(?>0)或反方向(?<0)上伸长为原来的∣?∣倍;

　当∣?∣<1时，表示向量a的有向线段在原方向(?>0)或反方向(?<0)上缩短为原来的∣?∣倍。

　数与向量的乘法满足下面的运算律

　结合律：(?a)?b=?(a?b)=(a?b)。

　向量对于数的分配律(第一分配律)：(?+?)a=?a+?a.

　数对于向量的分配律(第二分配律)：?(a+b)=?a+?b.

　数乘向量的消去律：① 如果实数?0且?a=?b，那么a=b。② 如果a?0且?a=?a，那么?=?。

　6、向量的的数量积

　定义：已知两个非零向量a,b。作OA=a,OB=b,则角AOB称作向量a和向量b的夹角，记作〈a,b〉并规定0?〈a,b〉?

　定义：两个向量的数量积(内积、点积)是一个数量，记作a?b。若a、b不共线，则a?b=|a|?|b|?cos〈a，b〉;若a、b共线，则a?b=+-∣a∣∣b∣。

　向量的数量积的坐标表示：a?b=x?x'+y?y'。

　向量的数量积的运算律

　a?b=b?a(交换律);

　(?a)?b=?(a?b)(关于数乘法的结合律);

　(a+b)?c=a?c+b?c(分配律);

　向量的数量积的性质

　a?a=|a|的平方。

　a?b 〈=〉a?b=0。

　|a?b|?|a|?|b|。

　7、向量的数量积与实数运算的主要不同点

　(1)向量的数量积不满足结合律，即：(a?b)?c?a?(b?c);例如：(a?b)^2?a^2?b^2。

　(2)向量的数量积不满足消去律，即：由 a?b=a?c (a?0)，推不出 b=c。

　(3)|a?b|?|a|?|b|

　(4)由 |a|=|b| ，推不出 a=b或a=-b。

　8、向量的向量积

　定义：两个向量a和b的向量积(外积、叉积)是一个向量，记作a?b。若a、b不共线，则a?b的模是：∣a?b∣=|a|?|b|?sin〈a，b〉;a?b的方向是：垂直于a和b，且a、b和a?b按这个次序构成右手系。若a、b共线，则a?b=0。

　(1)向量的向量积性质：

　∣a?b∣是以a和b为边的平行四边形面积。

　a?a=0。

　a‖b〈=〉a?b=0。

　(2)向量的向量积运算律

　a?b=-b?a;

　(?a)?b=?(a?b)=a?(?b);

　(a+b)?c=a?c+b?c.

　注：向量没有除法，?向量AB/向量CD?是没有意义的。

　(3)向量的三角形不等式

　∣∣a∣-∣b∣∣?∣a+b∣?∣a∣+∣b∣;

　① 当且仅当a、b反向时，左边取等号;

　② 当且仅当a、b同向时，右边取等号。

　∣∣a∣-∣b∣∣?∣a-b∣?∣a∣+∣b∣。

　① 当且仅当a、b同向时，左边取等号;

2017年全国一卷数学高考题，如图，答案最后为什么写m＞负一？

3cosa+4sina可以取值+/-5，在第三象限应为-5，因此-5-4-a=+/-17,解得a=-26/8;综合得a=-16,-26,8,18四个值。

参考答案为-16,18.只取第一象限点了

由前面推导可知，即由题设可知根的判别式=16(4K^2-m^2+1)>0，后面又求得k=-(m+1)/2

这样将k代入进去，4K^2-m^2+1>0

4ⅹ[-(m+1)/2]^2-m^2+1>0

化简得2m+2>0得m>-1

所以当且仅当m>-1时，根的判别式﹥0就是这样得来的。