关于函数高考题_数学函数高考题

1.高数：1.关于函数的连续性的问题，怎样找函数的间断点?

2.求10道高中数学函数类型的题目

3.求解一道高考数学填空题，题目如下，关于函数零点问题的，2014年天津文科14题，不胜感激啊，要思路和过程

4.关于函数的数学题!

5.问一题关于函数的数学题``后天就要高考嘞``

6.高中数学一轮复习，三角函数的问题？

7.2道高考题外加1道函数题

高考数学基础题二次函数、复合函数。?

1、二次函数。

二次函数解析式的三种形式：

一般式：f（x）＝ax2＋bx＋c（a≠0）。

顶点式：f（x）＝a（x－m）2＋n（a≠0）。

零点式：f（x）＝a（x－x1）（x－x2）（a≠0）。

辨明两个易误点：

对于函数y＝ax2＋bx＋c，要认为它是二次函数，就必须满足a≠0，当题目条件中未说明a≠0时，就要讨论a＝0和a≠0两种情况。

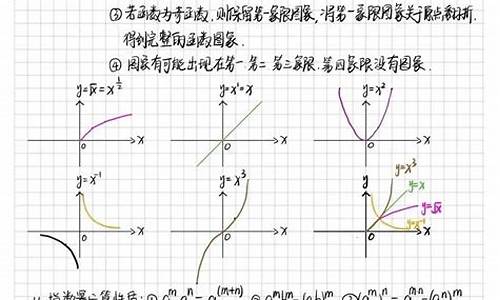
幂函数的图象一定会出现在第一象限内，一定不会出现在第四象限内，至于是否出现在第二、三象限内，要看函数的奇偶性；幂函数的图象最多只能同时出现在两个象限内；如果幂函数图象与坐标轴相交，则交点一定是原点。

2、复合函数。

设函数Y=f（u）的定义域为D，函数u=φ（x）的值域为Z，如果D∩Z，则y通过u构成x的函数，称为x的复合函数，记作Y=f（φ（x））。

x为自变量，y为因变量，而u称为中间变量。? 如等都是复合函数。? 就不是复合函数，因为任何x都不能使y有意义。由此可见，不是任何两个函数放在一起都能构成一个复合函数。

高考数学必备技巧：

1、三个“基本”：基本的概念要清楚，基本的规律要熟悉，基本的方法要熟练。

2、做完题目后一定要认真总结，做到举一反三，这样，以后遇到同一类的问题是就不会花费太多的时间和精力了。

3、一定要全面了解数学概念，不能以偏概全。

4、学习概念的最终目的是能运用概念来解决具体问题，因此，要主动运用所学的数学概念来分析，解决有关的数学问题。

5、要掌握各种题型的解题方法，在练习中有意识的地去总结，慢慢地培养适合自己的分析习惯。

6、要主动提高综合分析问题的能力，借助文字阅读去分析理解。

7、在学习中，要有意识地注意知识的迁移，培养解决问题的能力。

8、要将所学知识贯穿在一起形成系统，我们可以运用类比联系法。

9、将各章节中的内容互相联系，不同章节之间互相类比，真正将前后知识融会贯通，连为一体，这样能帮助我们系统深刻地理解知识体系和内容。

10、在数学学习中可以利用口诀将相近的概念或规律进行比较，搞清楚它们的相同点，区别和联系，从而加深理解和记忆。弄清数学知识间的相互联系，透彻理解概念，知道其推导过程，使知识条理化，系统化。

高数：1.关于函数的连续性的问题，怎样找函数的间断点?

此题是2009年山东高考试题（理科）第16题，原题是这样子：

已知定义在R上的奇函数f(x)满足f(x)=-f(x-4)，且在区间0，2上为增函数，若方程f(x)=m（m>0）在区间-8，8上有四个不同的根X1 X2 X3 X4,则X1+X2+X3+X4 =？

解定义在R上的奇函数f(x)满足f(x)=-f(x-4)，

所以f(x)= f(4-x)，函数图像关于直线x=2对称且f(0)=0.

由f(x-4) =- f(x)可知：f(x-8) =f(x)，函数周期为8.

又因函数在区间0，4上为增函数，所以函数在-4,0上也是增函数。

根据以上分析可以画出函数图像的简图。

方程f(x)=m（m>0）在区间-8，8上有四个不同的根X1，X2，X3，X4,

不妨设X1<X2<X3<X4,由对称性可知：X1+X2=-12，X3+X4=4，所以X1+X2+X3+X4=-8.

求10道高中数学函数类型的题目

答：

1）

-1<=x<=1，f(x)=x

x<-1或者x>1，f(x)=1

f(-1 -)=1，f(-1+)=-1，则x=-1是跳跃间断点

f(1-)=1，f(1+)=1，f(1)=1，则x=1是连续点

2）

x≠1，f(x)=x

x=1，f(x)=1/2

f(1-)=1，f(1+)=1

则x=1是可去间断点

求解一道高考数学填空题，题目如下，关于函数零点问题的，2014年天津文科14题，不胜感激啊，要思路和过程

1,若x是方程lgx+x=2的解，求x属于的区间。 2，把函数y=lg(2x)的图像a平移，得到函数y=lg(x-1)的图像，求a. 3,设函数f(x)=cos(x的绝对值+30度）（x是实数),求函数单调区间。 4，若函数f(x)=(X^2+bx+c)e^-x在（负无穷，-1），（1，正无穷）上单调递减，在（-1,1）单调递增，求b+c的值。 5，画出函数y=(2^x+1)\（2^x-1)的大致图像。 6，依次画出3^x,3^x+1,3^(x+1),3^x的绝对值的图像， 7，sin(x）经怎样变换得Asin(wx+b)+c,请用两种方法说明。 8，(ax+b)\(cx+d)的图像的中心对称点及变换方式。 9，f(x)图像关于原点坐标对称的图像恰好为y=3-2x的图像，求f（x). 10,e^x按照向量a=(2,3)平移得到新函数g(x），求g(x). 只是些容易题 ，做好这些，你就可以去做高考题啦！（结果如何，概不负责）但还是给点分额吧！

关于函数的数学题!

这个题主要考查函数零点个数的应用,利用数形结合是解决本题的关键,综合性较强,难度较大.

由y=f（x）-a|x|得f(x)=a|x|,利用数形结合即可得到结论。

解： 由y=f(x)-a|x|=0得f(x)=a|x|,做出函数y=f(x),y=a|x|的图像，当a≤0时，不满足条件，所以a>0.这是详细的答案已知函数f(x)=|x?+5x+4|,x≤0 ? 2|x-2|,x>0,若函数y=f(x)-a|x|恰有4个零点，则实数a的取值范围

仔细琢磨下答案，这种题基础还是很重要的，掌握好基础知识后，举一反三，分析的时候一种情况一种情况的来，不要搞乱了，希望对你有所帮助，加油~ 有用的话希望给个采纳哦！

问一题关于函数的数学题``后天就要高考嘞``

1.函数y=x^2-2x的定义域为{0,1,2,3},那么其值域为(A )

A.{-1,0,3} B.{0,1,2,3} C.{y|-1≤y≤3} D.{0≤y≤3}

把0,1,2,3分别代入y=x^2-2x，求出y分别为0，-1，0，3，所以选A

2.下列函数中,定义域为全体实数的是( D)

.y=√_____ x^2-x ( 下面的__符号是说明x^2-x在根号里 )

√

B.y=lg|x+1|

C.x/(x+2)^2-1

D.y=√(x+2)^2___ +1 ( +1不在根号里 )

A x^2-x≥0，不是R

B y=lg|x+1|，真数不等于0，x≠-1 不是R

C.x/(x+2)^2-1 分母不等于0， 不是R

D.y=√(x+2)^2___ +1 ( +1不在根号里 )，(x+2)^2≥0恒成立，所以是R

3.当0<a<1时,不等式a^2x-1>a(x-1)的解集为(dD)

A.x>1/a B.x>-1/a C.x<1/a Dx<-1/a

解(a^2-a)x>1-a,a-1≠0,a^2-a<0,,x<-1/a

4.下列为偶函数的是(D )

A.f(x)=√x B.f(x)=xcosx C.f(x)=x^2(-2<x≤2) D.f(x)=cosx+2

f(-x)=f(x),且定义域关于原点对称

C中定义域不关于原点对称

5.下列函数x>0时,为减函数的是( D)

A.y=2x-1 B.y=√x C.y=-1/x Dy=(2/3)^x

A.斜率>0为增

B.幂函数，指数大于0，为增

C.反比例函数，为减函数，但前面加了个负号，就为增

D.指数函数，底数小于1，为减函数

二.填空题

1.假设函数f(x-1)=x^2-1/2-3x,则f(0)=__-5/6_

x-1=0，x=1，代入即可

2.已知函数f(x)=log2a-1|x|在区间(-∞,0)上是增函数,则实数a的取值范围是

画图像就知道在(-∞,0)为增函数的是怎么样的

0<2a-1<1,-1/2<a<0_____ (2a-1在log的最下面)

3.函数y=(2x+1)/(3x-1)(x≠1/3)的值域是___y≠2/3（变换，求其反函数的定义域，用y来表示x就知道了）

4.已知函数f(x-2)=x^2+x+1,令t=x-2，则x=t+2

f(t)=_(t+2)^2+(t+2)+1,所以_f(x)=x^2+5x+7___

5.已知函数f(x)为奇函数且f(-4)=0,且当x>0是函数为增函数,则不等式f(x)>0的解集为

[_是奇函数，f(-4)=0，f(4)=0_，f(x)>f(4),增函数,所以解集为_{x|x>4}___

三.解答题

1.已知:{a,2}∩{1,2,3,2a+4}={6a-a^2-6},求:a的值

明显两个集合就有交集{2},因此6a-a^2-6=2

得到a=4或a=2，由于集合中元素不能重复，因此a=4

2.求函数y=lg(x^2-3x-40)/3^√|x+2|-6_没写明白__

3.判断函数f(x)=√9-x^2____/(|x+2|-2)的奇偶性. (_____符号说明前面的式子在根号里)

定义域为[-3,0)∪(0,3]关于原点对称

当x∈[-2,0)∪(0,2]时，f(x)=√(9-x^2)/(|x+2|-2)=√(9-x^2)/x

显然f(-x)=-f(x)

当x∈[-3,-2)时，f(x)=-√(9-x^2)/x

当x∈(2,3]时f(x)=√(9-x^2)/x,f(-x)=√(9-x^2)/(-x)=-f(x)

因此f(x)为奇函数

4.奇函数f(x)在定义域上(-1,1)是减函数,又f(1-a)+f(1-a^2)<0,求实数a的取值范围.

f(1-a)<-f(1-a^2)，因为奇函数f(x)，所以-f(1-a^2)=f(a^2-1)

定义域上(-1,1)是减函数，f(1-a)<f(a^2-1)

解三个不等式即可

(1)-1<1-a<1.

(2)-1<a^2-1<1.

(3)1-a>a^2-1

5.已知函数f(x)为二次函数,且f(1)=1,满足f(x+1)=f(x)=x+1,求二次函数f(x)的表达式.

条件有问题

高中数学一轮复习，三角函数的问题？

由于f是偶函数，所以在y轴两侧对称；

由于f(1/3)=0且f在正轴上递增，所以f在（-1/3，1/3）上小于0；

由上面的分析，我们要求x满足：

1，使log1/8 X有意义，即x〉0；

2，使log1/8 X大于1/3或者小于-1/3.

再注意到log1/8 X关于x单调减少，于是x的取值范围是

0<x<(1/8)^(1/3)=1/2,或者

x>(1/8)^(-1/3)=2

整理可得：（0，1/2）并上（2,正无穷）

2道高考题外加1道函数题

1、问题：诱导公式化简，α都必须看成锐角计算吗？为什么其他象限的角带进去不行？

答：1）诱导公式化简，把α都看成锐角，只是为了方便记忆，但没有规定必须看成锐角。

? 2）其他象限的角代入，也是完全正确的！

2、具体题目：

如果把α看做钝角，那么角（二分之π+α）是第三象限角，所以sin（二分之π+α）<0;

因为α看做钝角 所以cosα<0;

因此，sin（二分之π+α）＝cosα仍然成立！

3、

望采纳

第一题

解:a平方＋2ab+2ac+4bc=12

而:

2bc<=b平方+c平方

所以原式可化简为

a平方＋2ab+2ac+2bc+2bc=12

a平方＋2ab+2ac+2bc+b平方+c平方>=12

(a+b+c)平方>=12

a b c>0

a+b+c>=2根号3

第二题

解:

第一种情况:判别式<=0,=>a^2-4<=0,=>-2<=a<=2

第二种情况:判别式>=0,-a/2<=0,f(0)>=0,

=>a>=2

第三种情况:判别式>=0,-a/2>=1/2,f(1/2)>=0,

=>-5/2<=a<=-2

所以a的最小值为-5/2

第三题解：设f(x)=ax+b,则

f[f(x)]=a(ax+b)+b=a?x+ab+b=4x-1

因此a?=4.........(1)

ab+b=-1..........(2)

由（1）得a=±2.代入（2）式得：

（±2+1）b=-1,∴a=2时，b=-1/3; a=-2时，b=1.

故f(x)=2x-1/3或f(x)=-2x+1.

设f(x)=ax+b

为什么f(f(x))=af(x)+b ?

答：因为将括号内的f(x)看作一个整体，相当于一个x，此时的x=f(x),不知道你明白没？不明白的话可以给我发信息