高考题及坐标,高中坐标

1.2022年成人高考考试真题及答案解析-高起点《数学(文》？

2.2022年高考数学卷真题及答案解析(全国新高考1卷)

3.2008年数学成人高考数学题，那圆心坐标（4，0）这个怎么得来的。后来的也不看不懂！

4.求抛物线y=1/4x的平方的焦点坐标和准线方程

5.高中数学题型十六(坐标系与参数方程)

6.一道江苏省物理高考题！

题目已知O为坐标原点,F为椭圆C:x2+y22=1在y轴正半轴上的焦点,过F且斜率为-槡2的直线l与C交于A,B两点,点P满足?O→A+?O→B+?O→P=0.图1(Ⅰ)证明:点P在C上;(Ⅱ)设点P关于点O的对称点为Q,证明:A、P、B、Q四点在同一圆上.此题是2011年普通高等学校招生全国统一考试全国卷Ⅰ数

2022年成人高考考试真题及答案解析-高起点《数学(文》？

广西成考网分享：广西成人高考专升本高等数学一考试真题及参考答案

一、选择题：1～10小题，每小题4分，共40分.在每个小题给出的四个选项中，只有一项是符合题目要求的，把所选项前的字母填在题后的括号内.

1.

A.2/3 B.1 C.3/2 D.3

答案：C

2.设函数y=2x+sinx,则y/=

A.1-cosx B.1+cosx C.2-cosx D.2+cosx

答案：D

3.设函数y=ex-2,则dy=

A.ex-3dx B.ex-2dx C.ex-1dx D.exdx

答案：B

4.设函数y=(2+x)3，则y/=

A.(2+x)2 B.3(2+x)2 C.(2+x)4 D.3(2+x)4

答案：B

5.设函数y=3x+1,则y/=

A.0 B.1 C.2 D.3

答案：A

6.

A.ex B.ex-1 C.ex-1 D.ex+1

答案：A

7.

A.2x2+C B.x2+C C.1/2x2+C D.x+C

答案：C

8.

A.1/2 B.1 C.2 D.3

答案：C

9.设函数z=3x2y，则αz/αy=

A.6y B.6xy C.3x D.3X2

答案：D

10.

A.0 B.1 C.2 D.+∞

答案：B

二、填空题：11～20小题，每小题4分，共40分.把答案填在题中横线上.

11.

答案：e2

12.设函数y=x3,则y/=

答案：3x2

13.设函数y=(x-3)4,则dy=

答案：4(x-3)3dx

14.设函数y=sin(x-2)，则y"=

答案：-sin(x-2)

15.

答案：1/2ln|x|+C

16.

答案：0

17.过坐标原点且与直线(x-1)/3=(y+1)/2+(z-3)/-2垂直的平面方程为

答案：3x+2y-2z=0

18.设函数x=3x+y2，则dz=

答案：3dx+2ydy

19.微分方程y/=3x2的通解为y=

答案：x3+C

20.

答案：2

三、解答题：21-28题，共70分。解答应写出推理、演算步骤。

21.(本题满分8分)

22.(本题满分8分)

23.(本题满分8分)

求曲线y=x3-3x+5的拐点。

解：y/=3x2-3,y"=6x

令y"=0，解得x=0

当x<0时，y"0时，y">0

当x=0是，y=5

因此，点(0,5)为所给曲线的拐点

24.(本题满分8分)

25.(本题满分8分)

26.(本题满分10分)

设D为曲线y=x2与直线y=x所围成的有界平面图形，求D饶x轴旋转一周所得旋转体的体积V。

以上就是关于广西成人高考专升本高等数学一考试真题及参考答案的相关内容，考生如果想获取更多关于广西成人高考信息，如成考答疑、报考指南、成绩查询、历年真题、学习方法、广西成考专升本试题题库等，敬请关注广西成考网。

专升本有疑问、不知道如何总结专升本考点内容、不清楚专升本报名当地政策，点击底部咨询官网，免费领取复习资料： style="font-size: 18px;font-weight: bold;border-left: 4px solid #a10d00;margin: 10px 0px 15px 0px;padding: 10px 0 10px 20px;background: #f1dada;">2022年高考数学卷真题及答案解析(全国新高考1卷)

成考快速报名和免费咨询： 湖北成人高考网分享：2022年成人高考考试真题及答案解析-高起点《数学(文》 ，答案来自考生回忆(后期持续更新中)，仅供参考。 一、选择题(本大题17小题，每小题5分，共85分，在每小题给出四个选项中，只有一项是符合题目要求的)

1. 设集合M={Hx-2|2}，则MnN=( )

A. {x12}

C.{x2

答案：C

2. 设函数f(x)=x?，则f(x+1)( )

A.x?+2x+1 B.x?+2x C.x?+1 D.x?

答案A

3. 下列函数中，为奇函数的是( )

A.y=cox B.y=sinx C.y=2* D、y=x+1

答案B

4.设a是第三象限角，若cosa=-根号2/2，则sina=( )

A、根号2/2 B、1/2 C、-1/2 D、-根号2/2

答案D

5.函数y=x?+1(x≤0)的反函数是( )

A.y=-根号x-1(x≥1) B.y=根号x-1(x≥1) C.y-根号x-1(x≥0) D.-根号x-1

答案B

6.已知空间向量ijk为两两垂直的单位向量，向量a=2i+3j+mk,若|a|=根号13，则m=

A.-2 B.-1 C.0 D.1

答案C

7. 给出下列两个命题：

①如果一条直线与一个平面垂直，则该直线与该平面的任意一条直线垂直

②以二面角的棱上任意一点为端点，在二面角的两个面内分别做射线，则这两条射线所成的角为该二面角的平面角

则：

A ①②都为自命题 B ①为自命题，②为假命题 C ①为假，②为真 D ①②都假

答案B

二、填空题(本大题共4小题，每小题4分，共16分)

18. 点(4,5)关于直线y=x的对称点的坐标为(5,4) 。

19. log,3+10g,5/3-10g,5/8=(3)

20.某校学生参加一次科技知识竞赛，抽取了其中8位同学的分数作为样本数据如下：90,90,75,70,80,75,85,75，则该样本的平均数为(80)

21. 设函数f(x)=xsinx,，则f'(x)=sinx+xcosx

三、解答题(本大题共4小题，共49分，解答应写出推理、演算步骤)

22. 在△ABC中，B=120°，BC=4，△ABC的面积为4√3，求AC

答案AC=4√3

23. 已知a、b、c成等差数列，a、b、c+1成等比数列，若b=6，求a和c

答案a=4 ， c=8

24.已知直线1的斜率为1,1过抛物线L：x?=1/2y焦点，且与L交于A、B两点。

(1)求1与L的准线的交点坐标;

(2)求|AB|

答案更新中

25.设函数(x)=x3-4x

(1)求：f‘(2)

(2)求f(x)在区间[-1,2]的最大值与最小值

答案更新中

以上就是全部内容，更多内容请敬请关注湖北成考网(www.crgk.hb.cn)，更多湖北成考实时资讯，敬请关注猎考网。

成考有疑问、不知道如何总结成考考点内容、不清楚成考报名当地政策，点击底部咨询官网，免费领取复习资料： style="font-size: 18px;font-weight: bold;border-left: 4px solid #a10d00;margin: 10px 0px 15px 0px;padding: 10px 0 10px 20px;background: #f1dada;">2008年数学成人高考数学题，那圆心坐标（4，0）这个怎么得来的。后来的也不看不懂！

2022年高考数学依据数学课程标准命题，深化基础考查，突出主干知识，创新试题设计。下面是我为大家收集的关于2022年高考数学卷真题及答案解析(全国新高考1卷)。希望可以帮助大家。

高考数学卷真题

高考数学卷真题答案解析

高考数学知识点整理

一、直线方程.

1. 直线的倾斜角：一条直线向上的方向与轴正方向所成的最小正角叫做这条直线的倾斜角，其中直线与轴平行或重合时，其倾斜角为0，故直线倾斜角的范围是.

注：①当或时，直线垂直于轴，它的斜率不存在.

②每一条直线都存在惟一的倾斜角，除与轴垂直的直线不存在斜率外，其余每一条直线都有惟一的斜率，并且当直线的斜率一定时，其倾斜角也对应确定.

2. 直线方程的几种形式：点斜式、截距式、两点式、斜切式.

特别地，当直线经过两点，即直线在轴，轴上的截距分别为时，直线方程是：.

注：若是一直线的方程，则这条直线的方程是，但若则不是这条线.

附：直线系：对于直线的斜截式方程，当均为确定的数值时，它表示一条确定的直线，如果变化时，对应的直线也会变化.①当为定植，变化时，它们表示过定点(0，)的直线束.②当为定值，变化时，它们表示一组平行直线.

3. ⑴两条直线平行：

‖两条直线平行的条件是：①和是两条不重合的直线. ②在和的斜率都存在的前提下得到的. 因此，应特别注意，抽掉或忽视其中任一个“前提”都会导致结论的错误.

(一般的结论是：对于两条直线，它们在轴上的纵截距是，则‖，且或的斜率均不存在，即是平行的必要不充分条件，且)

推论：如果两条直线的倾斜角为则‖.

⑵两条直线垂直：

两条直线垂直的条件：①设两条直线和的斜率分别为和，则有这里的前提是的斜率都存在. ②，且的斜率不存在或，且的斜率不存在. (即是垂直的充要条件)

4. 直线的交角：

⑴直线到的角(方向角);直线到的角，是指直线绕交点依逆时针方向旋转到与重合时所转动的角，它的范围是，当时.

⑵两条相交直线与的夹角：两条相交直线与的夹角，是指由与相交所成的四个角中最小的正角，又称为和所成的角，它的取值范围是，当，则有.

5. 过两直线的交点的直线系方程为参数，不包括在内)

6. 点到直线的距离：

⑴点到直线的距离公式：设点，直线到的距离为，则有.

注：

1. 两点P1(x1,y1)、P2(x2,y2)的距离公式：.

特例：点P(x,y)到原点O的距离：

2. 定比分点坐标分式。若点P(x,y)分有向线段,其中P1(x1,y1),P2(x2,y2).则

特例，中点坐标公式;重要结论，三角形重心坐标公式。

3. 直线的倾斜角(0°≤<180°)、斜率:

4. 过两点.

当(即直线和x轴垂直)时，直线的倾斜角=，没有斜率

⑵两条平行线间的距离公式：设两条平行直线，它们之间的距离为，则有.

注;直线系方程

1. 与直线：Ax+By+C= 0平行的直线系方程是：Ax+By+m=0.( m?R, C≠m).

2. 与直线：Ax+By+C= 0垂直的直线系方程是：Bx-Ay+m=0.( m?R)

3. 过定点(x1,y1)的直线系方程是： A(x-x1)+B(y-y1)=0 (A,B不全为0)

4. 过直线l1、l2交点的直线系方程：(A1x+B1y+C1)+λ( A2x+B2y+C2)=0 (λ?R) 注：该直线系不含l2.

7. 关于点对称和关于某直线对称：

⑴关于点对称的两条直线一定是平行直线，且这个点到两直线的距离相等.

⑵关于某直线对称的两条直线性质：若两条直线平行，则对称直线也平行，且两直线到对称直线距离相等.

若两条直线不平行，则对称直线必过两条直线的交点，且对称直线为两直线夹角的角平分线.

⑶点关于某一条直线对称，用中点表示两对称点，则中点在对称直线上(方程①)，过两对称点的直线方程与对称直线方程垂直(方程②)①②可解得所求对称点.

注：①曲线、直线关于一直线()对称的解法：y换x，x换y. 例：曲线f(x ,y)=0关于直线y=x–2对称曲线方程是f(y+2 ,x –2)=0.

②曲线C: f(x ,y)=0关于点(a ,b)的对称曲线方程是f(a – x, 2b – y)=0.

2022年高考数学卷真题及答案解析(全国新高考1卷)相关 文章 ：

★ 2022全国甲卷高考数学文科试卷及答案解析

★ 2022年新高考Ⅱ卷数学真题试卷及答案

★ 2022高考全国甲卷数学试题及答案

★ 2022北京卷高考文科数学试题及答案解析

★ 2021年高考全国甲卷数学理科答案

★ 2022全国乙卷理科数学真题及答案解析

★ 2021新高考全国1卷数学真题及答案

★ 2022年全国乙卷高考理科数学题目与答案解析

★ 2022年全国乙卷高考数学(理科)试卷

★ 2022江西高考文科数学试题及答案

求抛物线y=1/4x的平方的焦点坐标和准线方程

对双曲线来说X^2与Y^2谁是正的，谁的分数线下边那个就是a^2（a的平方），负的那个下边是b^2，双曲线焦点坐标为（c，0）和（-c，0），并且双曲线的a,b,c满足a^2+b^2=c^2

a^2=4,? b^2=12, 所以c^2=16, ? c=4

所以焦点坐标就是（4,0）（-4,0），右焦点就是（4,0）

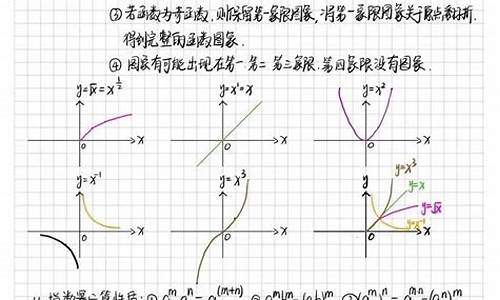
高中数学题型十六(坐标系与参数方程)

解：y=1/4x?

x?=4y

这个标准方程是焦点在y轴上，

焦点为（0,1）

准线为y=-1

抛物线焦点准线的求法：

1，化成标准方程：y?=2px或x?=2py的形式，

2，根据抛物线的定义，y?=2px焦点在x轴，焦点为（p/2，0），准线为x=-p/2

同理，x?=2py焦点在y轴，焦点为（0，p/2),准线为y=-p/2

抛物线：平面内，到定点与定直线的距离相等的点的轨迹叫做抛物线。其中定点叫抛物线的焦点，定直线叫抛物线的准线。

圆锥曲线：是高考重点考查的内容难度上易、中、难三档题都有，主要考查的内容是圆锥曲线的概念和性质，圆锥曲线在高考试题中占有稳定的较大的比例，且选择题、填空题和解答题都涉及到，客观题主要考察圆锥曲线的基本概念、标准方程及几何性质等基础知识和处理有关问题的基本技能、基本方法 。

一道江苏省物理高考题！

坐标系与参数方程、不等式选讲是全国卷的选做题，22题和23题，二者选其一。一般情况下，我会以坐标系与参数方程为主，要求学生对于23题要进行适当地练习，以防万一。

第22题主要考四种题型。

第一，普通方法，把题目中的全部曲线方程转化成直角坐标系下，利用解析几何的内容解决问题，属于简单的解析几何问题。

第二，圆与椭圆的参数方程，转化成三角函数求值域。

第三，直线的参数方程，t的几何意义，多数求解与线段长度相关的问题。

第四，极径与极角的几何意义，把题目中的全部曲线转化成极坐标系下进行相关计算。

历年高考真题多数考第一，第二，第四种题型，2018年全国卷2和全国卷3考到了第三种题型。

与线段长度相关的问题，有时可以用t的几何意义，有时也可以用极径的几何意义，区别在于后者试用范围是题目中的距离必须与某个点和极点的距离相关。

从图2可以看出，电场磁场刚好是交替出现，且存在的时间间隔都完全一致，通俗的说法就是有电场时就没磁场，有磁场就没有电场，磁场电场占用时间都是完全相同，有区别的是磁场方向会发生周期性变化。

分析完图再来看粒子的运动情况，粒子要做往复运动可以按猜想如下运动情景。

在t=T/2时刻，粒子经过电场加速，在t=T时刻运动到x轴上的某一个点，设为A点，且有一定的速度。

在t=T时刻电场消失，取而代之的是垂直向内的磁场，用左手定则可判定，洛伦兹力方向是向上，粒子向上偏转，做圆周运动，这个时期的时间段是T。

在t=2T时刻，粒子速度方向是x轴负方向，粒子在期间做了半个圆周运动，速度方向完全改变，设这个点为Q点，此时磁场消失，电场出现，粒子做减速运动。

在t=2.5T时刻，刚好达到y轴上设为B点。

在t=3T时刻，又回到Q点，电场消失，磁场出现，不过与上次不同的是磁场方向向外，

在t=4T时刻，粒子又沿着原来的轨迹回到A点。

如此粒子就可以在OAQB四点作往复运动。

粒子若能按这个设想往复运动，必须满足的条件就是“在t=2T时刻，粒子速度方向是x轴负方向，粒子在期间做了半个圆周运动”，除此之外，粒子都不可能作往复运动。运动轨迹见草图

所以时间段T恰好是圆周运动的半个周期，而周期公式T'=2πm/qB0

所以满足T=πm/qB0，B0=πm/qT