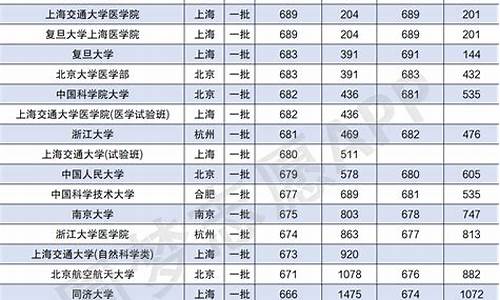
您现在的位置是: 首页 > 教育研究 教育研究
高考排序练习及答案_高考语文排序题解题技巧
tamoadmin 2024-06-09 人已围观
简介1.句子排序练习题2.排列组合问题排列组合的题目在分析过程中要做到“不重复,不遗漏”,因此,可以采用“互斥且完整”的方法来做分类列举,所谓“互斥”是指所列举的各种组合或排列情况各异,不存在重叠的情形,而“完整”则是指不遗漏任何可能的组合排列情形。以本题为例,假设5人分别为A、B、C、D、E,首先将所有排列组合分为两大类:1、A单独分派2、A与另外1人一起分派在1的情形下,另外4个人只能是两两组队,
1.句子排序练习题
2.排列组合问题
排列组合的题目在分析过程中要做到“不重复,不遗漏”,因此,可以采用“互斥且完整”的方法来做分类列举,所谓“互斥”是指所列举的各种组合或排列情况各异,不存在重叠的情形,而“完整”则是指不遗漏任何可能的组合排列情形。以本题为例,假设5人分别为A、B、C、D、E,
首先将所有排列组合分为两大类:
1、A单独分派
2、A与另外1人一起分派
在1的情形下,另外4个人只能是两两组队,一共有C(4,2)/2=3种组合方式
在2的情形下,可再划分为三小类情况,即A分别与C、D、E组队,那么在每一种情况下,余下三人也有3种组合方式,所以一共有3x3=9种组合方式
所以,这5人按要求分成三组,一共就有3+9=12种组合方式,而在每一种组合方式下,需要按3所学校进行全排列,即3!=6种排列方式,因此,最终就可以得到12x6=72种分配方式。
句子排序练习题
高考数学排列组合方法
排列组合问题联系实际生动有趣,但题型多样,思路灵活,因此解决排列组合问题,首先要认真审题,弄清楚是排列问题、组合问题还是排列与组合综合问题;其次要抓住问题的本质特征,采用合理恰当的方法来处理。
复习
1.分类计数原理(加法原理)
完成一件事,有
类办法,在第1类办法中有
种不同的方法,在第2类办法中有
种不同的方法,…,在第
类办法中有
种不同的方法,那么完成这件事共有:
种不同的方法.
2.分步计数原理(乘法原理)
完成一件事,需要分成
个步骤,做第1步有
种不同的方法,做第2步有
种不同的方法,…,做第
步有
种不同的方法,那么完成这件事共有:
种不同的方法.
3.分类计数原理分步计数原理区别
分类计数原理方法相互独立,任何一种方法都可以独立地完成这件事。
分步计数原理各步相互依存,每步中的方法完成事件的一个阶段,不能完成整个事件.
解决排列组合综合性问题的一般过程如下:
1.认真审题弄清要做什么事
2.怎样做才能完成所要做的事,即采取分步还是分类,或是分步与分类同时进行,确定分多少步及多少类。
3.确定每一步或每一类是排列问题(有序)还是组合(无序)问题,元素总数是多少及取出多少个元素.
4.解决排列组合综合性问题,往往类与步交叉,因此必须掌握一些常用的解题策略
一.特殊元素和特殊位置优先策略
例1.由0,1,2,3,4,5可以组成多少个没有重复数字五位奇数.
解:由于末位和首位有特殊要求,应该优先安排,以免不合要求的元素占了这两个位置.
先排末位共有
然后排首位共有
最后排其它位置共有
由分步计数原理得
位置分析法和元素分析法是解决排列组合问题最常用也是最基本的方法,若以元素分析为主,需先安排特殊元素,再处理其它元素.若以位置分析为主,需先满足特殊位置的要求,再处理其它位置。若有多个约束条件,往往是考虑一个约束条件的同时还要兼顾其它条件
练习题:7种不同的花种在排成一列的花盆里,若两种葵花不种在中间,也不种在两端的花盆里,问有多少不同的种法?
二.相邻元素捆绑策略
例2. 7人站成一排 ,其中甲乙相邻且丙丁相邻, 共有多少种不同的排法.
解:可先将甲乙两元素捆绑成整体并看成一个复合元素,同时丙丁也看成一个复合元素,再与其它元素进行排列,同时对相邻元素内部进行自排。由分步计数原理可得共有
种不同的排法
要求某几个元素必须排在一起的问题,可以用捆绑法来解决问题.即将需要相邻的元素合并为一个元素,再与其它元素一起作排列,同时要注意合并元素内部也必须排列.
练习题:某人射击8枪,命中4枪,4枪命中恰好有3枪连在一起的情形的不同种数为 20
三.不相邻问题插空策略
例3.一个晚会的节目有4个舞蹈,2个相声,3个独唱,舞蹈节目不能连续出场,则节目的出场顺序有多少种?
解:分两步进行第一步排2个相声和3个独唱共有
种,第二步将4舞蹈插入第一步排好的6个元素中间包含首尾两个空位共有种
不同的方法,由分步计数原理,节目的不同顺序共有
种
元素相离问题可先把没有位置要求的元素进行排队再把不相邻元素插入中间和两端
练习题:某班新年联欢会原定的5个节目已排成节目单,开演前又增加了两个新节目.如果将这两个新节目插入原节目单中,且两个新节目不相邻,那么不同插法的种数为 30
四.定序问题倍缩空位插入策略
例4.7人排队,其中甲乙丙3人顺序一定共有多少不同的排法
解:(倍缩法)对于某几个元素顺序一定的排列问题,可先把这几个元素与其他元素一起进行排列,然后用总排列数除以这几个元素之间的全排列数,则共有不同排法种数是:
(空位法)设想有7把椅子让除甲乙丙以外的四人就坐共有
种方法,其余的三个位置甲乙丙共有 1种坐法,则共有
种方法。
思考:可以先让甲乙丙就坐吗?
(插入法)先排甲乙丙三个人,共有1种排法,再把其余4四人依次插入共有 方法
定序问题可以用倍缩法,还可转化为占位插
空模型处理
练习题:10人身高各不相等,排成前后排,每排5人,要求从左至右身高逐渐增加,共有多少排法?
五.重排问题求幂策略
例5.把6名实习生分配到7个车间实习,共有多少种不同的分法
解:完成此事共分六步:把第一名实习生分配到车间有 7 种分法.把第二名实习生分配到车间也有7种分依此类推,由分步计数原理共有
种不同的排法
允许重复的排列问题的特点是以元素为研究对象,元素不受位置的约束,可以逐一安排各个元素的位置,一般地n不同的元素没有限制地安排在m个位置上的排列数为
种
练习题:
1. 某班新年联欢会原定的5个节目已排成节目单,开演前又增加了两个新节目.如果将这两个节目插入原节目单中,那么不同插法的种数为 42
2. 某8层大楼一楼电梯上来8名乘客人,他们到各自的一层下电梯,下电梯的方法
六.环排问题线排策略
例6. 8人围桌而坐,共有多少种坐法?
解:围桌而坐与坐成一排的不同点在于,坐成圆形没有首尾之分,所以固定一人
并从此位置把圆形展成直线其余7人共有(8-1)!种排法即
!
一般地,n个不同元素作圆形排列,共有(n-1)!种排法.如果从n个不同元素中取出m个元素作圆形排列共有
练习题:6颗颜色不同的钻石,可穿成几种钻石圈 120
七.多排问题直排策略
例7.8人排成前后两排,每排4人,其中甲乙在前排,丙在后排,共有多少排法
解:8人排前后两排,相当于8人坐8把椅子,可以把椅子排成一排.个特殊元素有
种,再排后4个位置上的特殊元素丙有
种,其余的5人在5个位置上任意排列有
种,则共有
种
一般地,元素分成多排的排列问题,可归结为一排考虑,再分段研究.
练习题:有两排座位,前排11个座位,后排12个座位,现安排2人就座规定前排中间的3个座位不能坐,并且这2人不左右相邻,那么不同排法的种数是 346
八.排列组合混合问题先选后排策略
例8.有5个不同的小球,装入4个不同的盒内,每盒至少装一个球,共有多少不同的装法.
解:第一步从5个球中选出2个组成复合元共有
种方法.再把4个元素(包含一个复合元素)装入4个不同的盒内有
种方法,根据分步计数原理装球的方法共有
解决排列组合混合问题,先选后排是最基本的指导思想.此法与相邻元素捆绑策略相似吗?
练习题:一个班有6名战士,其中正副班长各1人现从中选4人完成四种不同的任务,每人完成一种任务,且正副班长有且只有1人参加,则不同的选法有 192 种
九.小集团问题先整体后局部策略
例9.用1,2,3,4,5组成没有重复数字的五位数其中恰有两个偶数夹1,5在两个奇数之间,这样的五位数有多少个?
解:把1,5,2,4当作一个小集团与3排队共有
种排法,再排小集团内部共有
种排法,由分步计数原理共有
种排法.
小集团排列问题中,先整体后局部,再结合其它策略进行处理。
练习题:
1.计划展出10幅不同的画,其中1幅水彩画,4幅油画,5幅国画, 排成一行陈列,要求同一
品种的必须连在一起,并且水彩画不在两端,那么共有陈列方式的种数为
2. 5男生和5女生站成一排照像,男生相邻,女生也相邻的排法有
种
十.元素相同问题隔板策略
例10.有10个运动员名额,分给7个班,每班至少一个,有多少种分配方案?
解:因为10个名额没有差别,把它们排成一排。相邻名额之间形成9个空隙。在9个空档中选6个位置插个隔板,可把名额分成7份,对应地分给7个班级,每一种插板方法对应一种分法共有
种分法。
将n个相同的元素分成m份(n,m为正整数),每份至少一个元素,可以用m-1块隔板,插入n个元素排成一排的n-1个空隙中,所有分法数为
练习题:
1. 10个相同的球装5个盒中,每盒至少一有多少装法?
2 .
求这个方程组的自然数解的组数
十一.正难则反总体淘汰策略
例11.从0,1,2,3,4,5,6,7,8,9这十个数字中取出三个数,使其和为不小于10的偶数,不同的
取法有多少种?
解:这问题中如果直接求不小于10的偶数很困难,可用总体淘汰法。这十个数字中有5个偶数5个奇数,所取的三个数含有3个偶数的取法有
,只含有1个偶数的取法有
,和为偶数的取法共有
。再淘汰和小于10的偶数共9种,符合条件的取法共有
有些排列组合问题,正面直接考虑比较复杂,而它的反面往往比较简捷,可以先求出它的反面,再从整体中淘汰.
练习题:我们班里有43位同学,从中任抽5人,正、副班长、团支部书记至少有一人在内的
抽法有多少种?
十二.平均分组问题除法策略
例12. 6本不同的书平均分成3堆,每堆2本共有多少分法?
解: 分三步取书得
种方法,但这里出现重复计数的现象,不妨记6本书为ABCDEF,若第一步取AB第二步取CD,第三步取EF该分法记为(AB,CD,EF),则
中还有(AB,EF,CD),(CD,AB,EF),(CD,EF,AB)(EF,CD,AB),(EF,AB,CD)共有
种取法 ,而这些分法仅是(AB,CD,EF)一种分法,故共有
种分法。
平均分成的组,不管它们的顺序如何,都是一种情况,所以分组后要一定要除以
(
为均分的组数)避免重复计数。
练习题:
1 将13个球队分成3组,一组5个队,其它两组4个队, 有多少分法?(
)
2.10名学生分成3组,其中一组4人, 另两组3人但正副班长不能分在同一组,有多少种不同的
分组方法 (1540)
3.某校高二年级共有六个班级,现从外地转 入4名学生,要安排到该年级的两个班级且每班安
排2名,则不同的安排方案种数为______(
)
十三. 合理分类与分步策略
例13.在一次演唱会上共10名演员,其中8人能能唱歌,5人会跳舞,现要演出一个2人唱歌2人伴舞的节目,有多少选派方法
解:10演员中有5人只会唱歌,2人只会跳舞3人为全能演员。选上唱歌人员为标准进行研究
只会唱的5人中没有人选上唱歌人员共有
种,只会唱的5人中只有1人选上唱歌人员
种,只会唱的5人中只有2人选上唱歌人员有
种,由分类计数原理共有
种。
解含有约束条件的排列组合问题,可按元素的性质进行分类,按事件发生的连续过程分步,做到标准明确。分步层次清楚,不重不漏,分类标准一旦确定要贯穿于解题过程的始终。
练习题:
1.从4名男生和3名女生中选出4人参加某个座 谈会,若这4人中必须既有男生又有女生,则不同的选法共有34
2. 3成人2小孩乘船游玩,1号船最多乘3人, 2号船最多乘2人,3号船只能乘1人,他们任选2只船或3只船,但小孩不能单独乘一只船, 这3人共有多少乘船方法. (27)
本题还有如下分类标准:
*以3个全能演员是否选上唱歌人员为标准
*以3个全能演员是否选上跳舞人员为标准
*以只会跳舞的2人是否选上跳舞人员为标准 都可经得到正确结果
十四.构造模型策略
例14. 马路上有编号为1,2,3,4,5,6,7,8,9的九只路灯,现要关掉其中的3盏,但不能关掉相邻的2盏或3盏,也不能关掉两端的2盏,求满足条件的关灯方法有多少种?
解:把此问题当作一个排队模型在6盏亮灯的5个空隙中插入3个不亮的灯有
种
一些不易理解的排列组合题如果能转化为非常熟悉的模型,如占位填空模型,排队模型,装盒模型等,可使问题直观解决
练习题:某排共有10个座位,若4人就坐,每人左右两边都有空位,那么不同的坐法有多少种?(120)
十五.实际操作穷举策略
例15.设有编号1,2,3,4,5的五个球和编号1,2,3,4,5的五个盒子,现将5个球投入这五个盒子内,要求每个盒子放一个球,并且恰好有两个球的编号与盒子的编号相同,有多少投法
解:从5个球中取出2个与盒子对号有
种还剩下3球3盒序号不能对应,利用实际操作法,如果剩下3,4,5号球, 3,4,5号盒3号球装4号盒时,则4,5号球有只有1种装法,同理3号球装5号盒时,4,5号球有也只有1种装法,由分步计数原理有
种
3号盒 4号盒 5号盒
对于条件比较复杂的排列组合问题,不易用公式进行运算,往往利用穷举法或画出树状图会收到意想不到的结果
练习题:
1.同一寝室4人,每人写一张贺年卡集中起来,然后每人各拿一张别人的贺年卡,则四张贺年卡不同的分配方式有多少种? (9)
2.给图中区域涂色,要求相邻区 域不同色,现有4种可选颜色,则不同的着色方法有 72种
十六. 分解与合成策略
例16. 30030能被多少个不同的偶数整除
分析:先把30030分解成质因数的乘积形式30030=2×3×5 × 7 ×11×13
依题意可知偶因数必先取2,再从其余5个因数中任取若干个组成乘积,
所有的偶因数为:
练习:正方体的8个顶点可连成多少对异面直线
解:我们先从8个顶点中任取4个顶点构成四体共有体共
,每个四面体有
分解与合成策略是排列组合问题的一种最基本的解题策略,把一个复杂问题分解成几个小问题逐一解决,然后依据问题分解后的结构,用分类计数原理和分步计数原理将问题合成,从而得到问题的答案 ,每个比较复杂的问题都要用到这种解题策略
3对异面直线,正方体中的8个顶点可连成
对异面直线
十七.化归策略
例17. 25人排成5×5方阵,现从中选3人,要求3人不在同一行也不在同一列,不同的选法有多少种?
解:将这个问题退化成9人排成3×3方阵,现从中选3人,要求3人不在同一行也不在同一列,有多少选法.这样每行必有1人从其中的一行中选取1人后,把这人所在的行列都划掉,如此继续下去.从3×3方队中选3人的方法有
种。再从5×5方阵选出3×3方阵便可解决问题.从5×5方队中选取3行3列有
选法所以从5×5方阵选不在同一行也不在同一列的3人有
选法。
处理复杂的排列组合问题时可以把一个问题退化成一个简要的问题,通过解决这个简要的问题的解决找到解题方法,从而进下一步解决原来的问题
练习题:某城市的街区由12个全等的矩形区组成其中实线表示马路,从A走到B的最短路径有多少种?(
)
十八.数字排序问题查字典策略
例18.由0,1,2,3,4,5六个数字可以组成多少个没有重复的比324105大的数?
解:
数字排序问题可用查字典法,查字典的法应从高位向低位查,依次求出其符合要求的个数,根据分类计数原理求出其总数。
练习:用0,1,2,3,4,5这六个数字组成没有重复的四位偶数,将这些数字从小到大排列起来,第71个数是 3140
十九.树图策略
例19.
人相互传球,由甲开始发球,并作为第一次传球,经过
次传求后,球仍回到甲的手中,则不同的传球方式有______
对于条件比较复杂的排列组合问题,不易用
公式进行运算,树图会收到意想不到的结果
练习: 分别编有1,2,3,4,5号码的人与椅,其中
号人不坐
号椅(
)的不同坐法有多少种?
二十.复杂分类问题表格策略
例20.有红、黄、兰色的球各5只,分别标有A、B、C、D、E五个字母,现从中取5只,要求各字母均有且三色齐备,则共有多少种不同的取法
红
1
1
1
2
2
3
黄
1
2
3
1
2
1
兰
3
2
1
2
1
1
取法
解:
一些复杂的分类选取题,要满足的条件比较多, 无从入手,经常出现重复遗漏的情况,用表格法,则分类明确,能保证题中须满足的条件,能达到好的效果.
二十一:住店法策略
解决“允许重复排列问题”要注意区分两类元素:一类元素可以重复,另一类不能重复,把不能重复的元素看作“客”,能重复的元素看作“店”,再利用乘法原理直接求解.
例21.七名学生争夺五项冠军,每项冠军只能由一人获得,获得冠军的可能的种数有 .
分析:因同一学生可以同时夺得n项冠军,故学生可重复排列,将七名学生看作7家“店”,五项冠军看作5名“客”,每个“客”有7种住宿法,由乘法原理得7
种.
小结
本节课,我们对有关排列组合的几种常见的解题策略加以复习巩固。排列组合历来是学习中的难点,通过我们平时做的练习题,不难发现排列组合题的特点是条件隐晦,不易挖掘,题目多变,解法独特,数字庞大,难以验证。同学们只有对基本的解题策略熟练掌握。根据它们的条件,我们就可以选取不同的技巧来解决问题.对于一些比较复杂的问题,我们可以将几种策略结合起来应用把复杂的问题简单化,举一反三,触类旁通,进而为后续学习打下坚实的基础。
排列组合问题
一、中考真题
1、(2009年甘肃天水市中考试题)依次填入文段横线处,恰当的一组句子是 ( )
___________,你尽可流动明眸,欣赏白云蓝天,飞流急湍;_________,你尽可闭目凝神,倾听莺歌燕舞,春水潺潺;________,你尽可翕动鼻翼,呼吸牡丹的浓香,黄菊的清爽;__________,你尽可品评自娱,把玩深尝。
①文学是一座姹紫嫣红的百花园;②文学是一杯回味无穷的香茗;③文学是一幅意境高远的中国画;④文学是一首清脆圆润的古曲。
A.①③④② B.③④①②
C.④③②① D.②①③④
答案:B
透视:这是一道选择题。试题材料以文学为描写对象,以排比嵌套比喻的手法,从四个方面进行描述。试题抽去每一分句的第一句话(这四句话分别从四个角度对文学设喻)列于题后,打乱顺序后让考生进行归位选择。解答此题,可从视觉、听觉、嗅觉、感觉四个方面入手,将每一个喻体与其后的描述联系起来,看它们是否意蕴连贯。
2.(2009年浙江杭州市中考试题)填入下面横线上的句子,排列恰当的一项是 (A )
千岛湖畔的油茶树,生就了一副怪脾气。________冷寂的秋天在油茶花的映衬下,多了好些妩媚。同在秋天开放的菊花,古往今来,受到多少人的歌吟和追捧。而油茶花却安贫乐道,不慕虚华,更有君子气。
①这花,如秋叶般静美,不慌不忙,从从容容绽放。
②放眼望去,像一层薄薄的初雪覆压,又如一场浓霜骤然降临。
③她不羡慕春的热闹、夏的灿烂,却选择在落木萧萧的秋,开出甜蜜淡雅的花。
④白色的花瓣,**的花蕊,你挨我,我挨你,层层缀满枝头。
A.③①④② B.④①②③
C.③④①② D.④②③①
3.(2009年四川内江市中考试题)依次填入下段文字括号里的句子,最恰当的一组是 (A )
台湾漫画家蔡志忠说:“如果拿橘子来比喻人生,一种橘子大而酸,一种橘子小而甜,一些人( ),( )。而我( ),( )。”
A。拿到大的就会抱怨酸 拿到甜的就会抱怨小 拿到了小橘子就会庆幸它是甜的 拿到酸橘子就会感谢它是大的
B。拿到了小橘子就会庆幸它是甜的 拿到酸橘子就会感谢它是大的 拿到大的就会抱怨酸 拿到甜的就会抱怨小
C。拿到大的就会抱怨酸 拿到了小橘子就会庆幸它是甜的 拿到甜的就会抱怨小 拿到酸橘子就会感谢它是大的
D。拿到甜的就会抱怨小 拿到酸橘子就会感谢它是大的 拿到大的就会抱怨酸 拿到了小橘子就会庆幸它是甜的
4.(2009年江苏扬州市中考试题)依次填入下列文字横线处最恰当的一组是( D)
让我们对所有的苦难心存感激,因为,生命_____,思想______,意志______。
①总是在徘徊和失意中成熟 ②总是在挫折和磨难中茁壮 ③总是在残酷和无情中坚强
A.②③① B.③②① C.①②③ D.②①③
5.(2009年广东深圳市中考试题)请选出下列句子排序正确的一项 (A )
①博士除授予学官,还授予一些有专门技艺、专门学问的职官,如魏晋以后的太医博士、天文博士、历博士、卜博士等。
②秦始皇时,博士只作政府顾问。
③唐宋以后,社会上对从事某种职业的人也俗称博士,如“茶博士”“酒博士”等。
④汉代以后,博士开始任学官,担任教学工作。
⑤博士在我国古代是个官名,最早出现在战国时代。
A.⑤②④①③ B.①⑤②④③
C.⑤④③①② D.①④②③⑤
Ⅱ专项模拟训练
1.下面宣传语中四字短语之间衔接不恰当的一项是( C)
A。点燃激情,传递梦想,凝聚爱心,支援灾区(街头横幅)
B。保护草坪,请勿踩踏,爱护花木,请勿采摘(公园告示牌)
C。反对邪教,关爱家庭,珍惜生命,崇尚科学(社区标语牌)
D。润肺化痰,止咳平喘,护喉利咽,生津补气(药品广告)
2.根据语境,空白处应填入的语句最恰当的一项是(C )
这次来信所说的痛苦,我都理会的;我很同情,我愿意尽量安慰你,鼓励你。克利斯朵夫不是经过多少回这种情形吗?
A。他是一切艺术家的缩影与结晶吗?
B。他难道不是一切艺术家的缩影与结晶吗?
C。他不是一切艺术家的缩影与结晶吗?
D。一切艺术家的缩影与结晶就是他。
3.依次填入下面文字横线上的句子,与上下文衔接最恰当的一项是(C )
天地有大美,于简单处得;人生有大疲惫,在复杂处藏。人,_______;_______。这反映出的现实问题是:更多的人,_______,_________。
①要活出简单来不容易 ②一简单就快乐,但快乐的人寥寥无几 ③一复杂就痛苦,可痛苦的人熙熙攘攘④要活出复杂来却很简单
A.①②④③ B.①④②③
C.②③①④ D.②③④①
4.在下面语段空白处依次填入一组句子,正确的一项是 (B )
映日荷花,接天莲叶,亭亭莲蓬,柔嫩玉藕,无不牵惹诗情,引人遐思。让我们学做莲叶的事业吧, ;让我们学做荷花的事业吧,_______;让我们学做莲子的事业吧,_______;让我们学做藕的事业吧,______。
①把寂寞留给自己 ②把芬芳奉献给他人 ③以苦心孕育未来 ④以宽阔拥抱生活
A.②①④③ B.④②③①
C.③②④① D.①④③②
5.下列句子顺序排列正确的一项是 (C )
①水立方采用的ETFE膜,只有一张牛皮纸厚,捧在手上轻若鸿毛。②此外,它的耐火性、耐热性也非常出色。③然而这种膜的耐压性非常强,正常状态下,一辆小汽车开过去膜都不会被压破。④国家游泳中心“水立方”是世界上唯一一个完全由膜结构来进行全封闭的大型公共建筑。⑤ETFE膜的延展性也很好,它可以被拉伸到自身的三倍到四倍也不会断裂。
A.①④⑤③② B.①⑤④②③
C.④①③⑤② D.④⑤③①②
“选元”(从n类个不同元素中每次取出m个元素)是排列和组合两个概念的共同属性,而“排序”(是否将取出的m个元素按照一定的顺序排成一列)是排列和组合两个概念的不同属性.
你根据以上的定义可以知道,排列和组合都是从一个大范围里面取东西,区别是排列取出东西要再按顺序排列,组合取出的东西相互间没有顺序关系
举个简单的例子,
1.从20个人中选3个人,不同选发是?
这时用的是组合,因为取出3个人后,没有要求他们再按什么排列,也就是对他们的位置没有限定
2,从20个人里选3个,而后按身高由高到矮排队,有多少不同方法?
这时用排列,因为从20个人里选3个后,还要按高矮排列,这时题2比题1的不同之处,按高矮排,就说明,题目是对3个人的顺序是有限定,这时用排列
同理,按高矮排还可以改成按体重,视力,分数,等等等等
自我感觉学的时候你知道概念和会做题是两会事,因为题目中有很多技巧,光知道概念是没法做的
比如以下
一、合理分类与准确分步法
解含有约束条件的排列组合问题,应按元素性质进行分类,按事情发生的连续过程分步,作到分类标准明确,分步层次清楚,不重不漏。
例1 、五个人排成一排,其中甲不在排头,乙不在排尾,不同的排法有 ( )
A.120种 B.96种 C.78种 D.72种
选C
二、正难反易转化法
对于一些生疏问题或直接求解较为复杂或较为困难问题,从正面入手情况较多,不易解决,这时可从反面入手,将其转化为一个简单问题来处理。
例2、 马路上有8只路灯,为节约用电又不影响正常的照明,可把其中的三只灯关掉,但不能同时关掉相邻的两只或三只,也不能关掉两端的灯,那么满足条件的关灯方法共有多少种?
分析: 关掉第1只灯的方法有6种,关第二只,第三只时需分类讨论,十分复杂。若从反面入手考虑,每一种关灯的方法对应着一种满足题设条件的亮灯与关灯的排列,于是问题转化为“在5只亮灯的6个空中插入3只暗灯”的问题。
三、混合问题“先选后排”
对于排列组合混合问题,可先选出元素,再排列。
例 3、 4个不同小球放入编号为1,2,3,4的四个盒中,恰有一空盒的方法有多少种?
因有一空盒,故必有一盒子放两球,他们是先选的,答案144
四、特殊元素“优先安排法”
对于带有特殊元素的排列组合问题,一般应先考虑特殊元素,再考虑其它元素。
例4、 用0,2,3,4,5,五个数字,组成没有重复数字的三位数,其中偶数共有( )。
A24个 B。30个 C。40个 D。60个
[分析]由于该三位数为偶数,故末尾数字必为偶数,又因为0不能排首位,故0就是其中的“特殊”元素,应该优先安排,按0排在末尾和0不排在末尾分两类 选B
五、总体淘汰法
对于含有否定字眼的问题,可以从总体中把不符合要求的除去,此时需注意不能多减,也不能少减。
例子4可以按这个方法做
六、局部问题“整体优先法”
对于局部排列问题,可先将局部看作一个元与其余元素一同排列,然后在进行局部排列。
例5、7人站成一排照相,要求甲乙两人之间恰好隔三人的站法有多少种?
分析: 甲、乙及间隔的3人组成一个“小整体”,这3人可从其余5人中选,这是第一步要做的 答案720
七、相邻问题一“元”法
对于某几个元素要求相邻的排列问题,可将相邻的元素看作一个“元”与其他元素排列,然后在对“元”内部元素排列。
例6、 7人站成一排照相,甲、乙、丙三人相邻,有多少种不同排法?
分析: 把甲、乙、丙三人看作一个“元”,与其余4人共5个元作全排列答案7200种
八、不相邻问题“插空法”
对于某几个元素不相邻的排列问题,可先将其他元素排好,再将不相邻元素在已排好的元素之间及两端空隙中插入即可。
例7、在例6中, 若要求甲、乙、丙不相邻,则有多少种不同的排法?
先将4人排好,出现5个空,甲乙两人进5个空中的3个 答案1400
九。构造模型 “隔板法”
对于较复杂的排列问题,可通过设计另一情景,构造一个隔板模型来解决问题。
十一、分排问题“直排法”
把几个元素排成前后若干排的排列问题,若没有其它的特殊要求,可采取统一排成一排的方法来处理。
例10、7个人坐两排座位,第一排3个人,第二排坐4个人,则不同的坐法有多少种?
分析:7个人可以在前两排随意就坐,再无其它条件,故两排可看作一排来处理
近几年高考选择还出现一种题,列举,他用排列组合公式算不了,可是也算排列组合中的一种,这时你只能将可能一种一种列出了